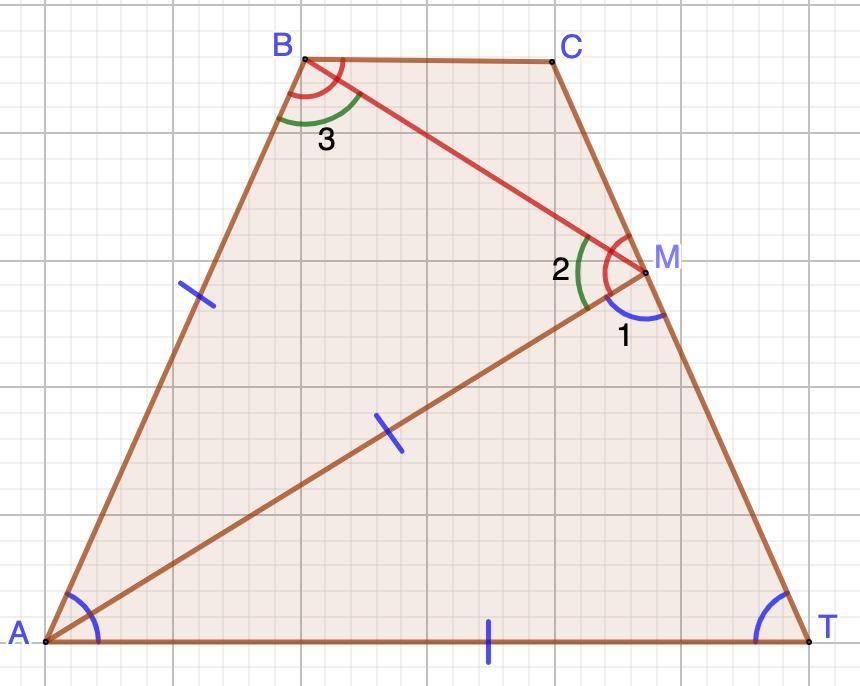
на боковой стороне CT трапеции ABCT отмечена такая точка M что AB=AT=AM=CT, докажите что треугольник BCM равнобедренный​

Пошаговое объяснение:

Дано: АВСТ - трапеция

AB=AT=AM=CT

Доказать: ΔВСМ - равнобедренный.

Доказательство:

1. Рассмотрим АВСТ.

АВ = СТ (условие)

⇒ АВСТ - равнобедренная трапеция.

• В равнобедренной трапеции углы при основаниях равны.

⇒ ∠А = ∠Т.

• В трапеции углы, прилежащие к боковой стороне равны в сумме 180°.

⇒ ∠В = 180° - ∠А

2. Рассмотрим ΔАМТ.

АТ = АМ (условие)

⇒ ΔАМТ - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠Т = ∠1

3.     Сумма смежных углов равна 180°.

∠АМС = 180°-∠1 (смежные)

 ∠В     = 180° - ∠А (п.1)

∠А = ∠Т = ∠1 (п.1,2)

⇒ ∠В = ∠АМС

4. Рассмотрим ΔАВМ.

АВ = АМ (условие)

⇒ ΔАВМ - равнобедренный.

⇒ ∠2 = ∠3 (при основании р/б треугольника)

5. Рассмотрим ΔВСМ.

∠МВС = ∠В - ∠3

∠ВМС = ∠АМС-∠2

⇒ ∠МВС = ∠МВС

• Если в треугольнике равны два угла, то этот треугольник равнобедренный.

⇒ ΔВСМ - равнобедренный.