Предмет: Геометрия,
автор: DankaToy
найдите боковое ребро правильной четырехугольной пирамиды, если объем равен 4 см2, а сторона основания равна 2 см
Ответы
Автор ответа:
0
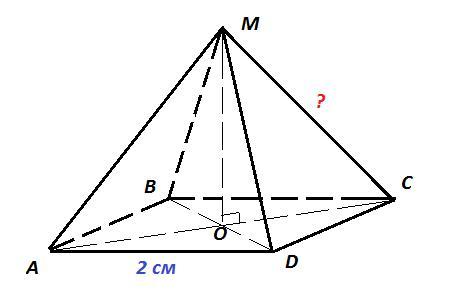
MABCD - правильная пирамида, V=4 см³, AB=BC=CD=AD=2 см
MO = 3 см
Диагональ квадрата основания
AC = AD · √2 = 2√2 см
Диагонали квадрата делятся точкой пересечения пополам
OC = AC : 2 = 2√2 : 2 = √2 см
ΔMOC - прямоугольный, ∠MOC=90°, OC=√2 см, MO=3 см
Теорема Пифагора
MC² = MO² + OC² = 3² + √2² = 11 ⇒ MC = √11 см
Ответ: √11 см
Приложения:
Интересные вопросы
Предмет: Математика,
автор: Veolwy
Предмет: Информатика,
автор: Аноним
Предмет: Математика,
автор: xogox78099
Предмет: Химия,
автор: Katya55