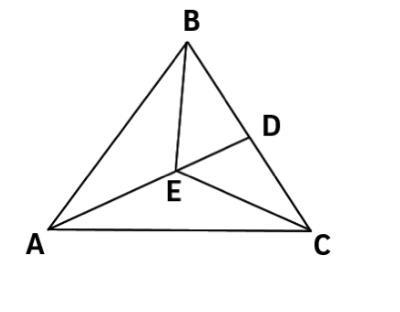
Задание 5 (25 баллов). На рисунке ∠ BAE = ∠ CAE, ∠ BED = ∠ CED. Сколько пар равных треугольников на рисунке? Запишите доказательство равенства для каждой пары.

Ответ:

3 пары равных треугольников дна рисунке.

Объяснение:

1.

∠AEB = 180° - ∠BED, так как эти углы смежные,

∠AEC = 180° - ∠CED, так как эти углы смежные,

по условию ∠BED = ∠CED, значит и ∠АЕВ = ∠АЕС.

2.

Рассмотрим ΔАЕВ и ΔАЕС:

∠ВАЕ = ∠САЕ по условию,

∠АЕВ = ∠АЕС (доказано в п. 1),

АЕ - общая сторона, значит

ΔАЕВ = ΔАЕС по стороне и двум прилежащим к ней углам.

В равных треугольниках против равных углов лежат равные стороны, следовательно АВ = АС и ВЕ = СЕ.

3.  

Рассмотрим ΔBED и ΔCED:

ВЕ = СЕ (доказано в п. 2),

∠BED = ∠CED по условию,

ED - общая сторона, значит

ΔBED = ΔCED по двум сторонам и углу между ними.

Из равенства треугольников следует, что BD = CD.

4.

Рассмотрим ΔABD и ΔACD:

АВ = АС (доказано в п. 2),

BD = CD (доказано в п. 3),

AD - общая сторона, значит

ΔABD и ΔACD по трем сторонам.