Предмет: Алгебра,
автор: Ncddekster1
 (sin2x + sinx) -2cosx
(sin2x + sinx) -2cosx  1 , если x ∈ [0; π]
1 , если x ∈ [0; π]
Ответы
Автор ответа:
1
Ответ:
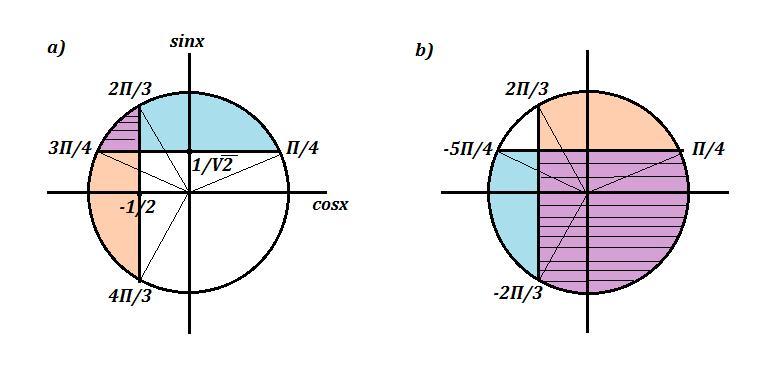
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: yxduubfcy
Предмет: Английский язык,
автор: foxypro
Предмет: Английский язык,
автор: катя2857
Предмет: Право,
автор: retq
Предмет: Алгебра,
автор: fany1028