Предмет: Алгебра, автор: Аноним

Нужно решить задачу

Приложения:

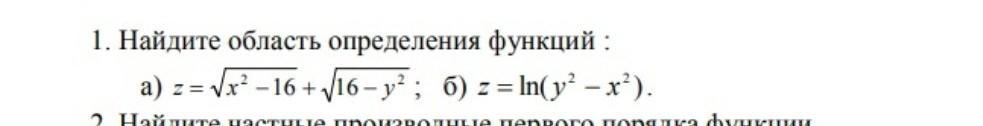
Аноним: не нужно решать

Ответы

Автор ответа: sangers1959

1

Ответ:

Объяснение:

1.

$a)\ z=\sqrt{x^2-16} +\sqrt{16-y^2}. \\$

ОДЗ:

$\left \{ {{x^2-16\geq 0} \atop {16-y\geq 0\ |*(-1)}} \right. \ \ \ \ \ \ \left \{ {{x^2-4^2\geq 0} \atop {y^2-4^2\leq 0}} \right. \ \ \ \ \ \ \left \{ {{(x+4)(x-4)\geq 0} \atop {(y+4)(y-4)\leq 0}} \right. \ \ \ \ \ \left \{ {{x\in(-\infty;-4]U[4;+\infty)} \atop {y\in[-4;4]}} \right. .$

$b)\ z=ln(y^2-x^2).$

ОДЗ:

$y^2-x^2>0\\(y+x)(y-x)>0\\y\in(-\infty;-x)U(x;+\infty).\\(y+x)(y-x)>0\ |*(-1)\\(x+y)(x-y)<0\\x\in(-y;y).$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: Ольга0602

что можно сказать о глаголах ,которыми выражены сказуемые?Эти глаголы 1 спряжения или 2 спряжения?Он пролетел , он опустился . Почему .

2 года назад

Предмет: Українська мова, автор: Мирка123

5 речень про дуб в науковом стиле и в художним стиле

2 года назад

Предмет: Русский язык, автор: bakis

Номер 3, пожалуйста, поскорее

2 года назад

Предмет: Алгебра, автор: vasafeda

Решите пример (10балов) :

8 лет назад

Предмет: Математика, автор: kamilla99044

сделайте пожалуйста срочно!!!

8 лет назад