Предмет: Алгебра,
автор: aleksandradyabina
Даны вершины треугольника А(-3;-4) В (-5;-2); С(1;-4). Составить уравнение высоты АD и найти координаты точки D - точки пересечения высоты АD и стороны BC.
Ответы
Автор ответа:
2
Ответ:
AD ⊥ BC ⇒ ВС - нормальный вектор для AD . Уравнение прямой через нормальный вектор имеет вид;
Найдём уравнение ВС через направляющий вектор ВС .
Точку пересечения AD и BC найдём из системы
Точка пересечения имеет координаты (-2,6 ; -2,8) .
Приложения:

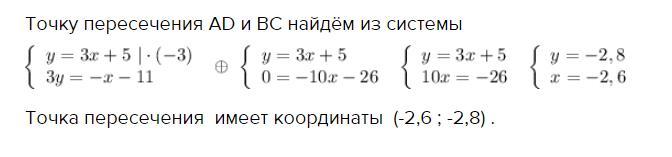
aleksandradyabina:
Не видно ничего(
Вы можете мне сделать скрин и прислать в сообщения?
Не видно уравнений
см скрин
Спасибо большое
Интересные вопросы
Предмет: Русский язык,
автор: baxruzik2008
Предмет: Русский язык,
автор: толя101
Предмет: Русский язык,
автор: kretsuapolina1218
Предмет: Математика,
автор: Diman1008
Предмет: Биология,
автор: vladanigmatyllina