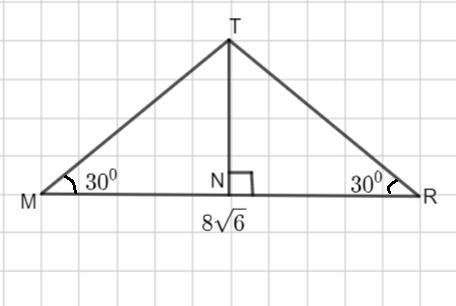
Реши равнобедренный треугольник MTR , если углы при основании равны 30° , а длина основания MR= 8 в корне 6

Ответ:

∠M=30°, ∠R=30°, ∠Т=120°,      

Пошаговое объяснение:

Рассмотрим  Δ MTR - равнобедренный.

В равнобедренном треугольнике углы при сновании равны.

Значит,

∠M= ∠R=30°.

Так как сумма углов треугольника равна 180°, то

∠Т= 180°-(30°+30°)=180°-60°=120°

По условию основание

.

В равнобедренном треугольнике проведем высоту к основанию, она является медианой. Значит,

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Рассмотрим  Δ MNT - прямоугольный.

Так как треугольник равнобедренный, то