Предмет: Математика, автор: engulatovalena

Упростите:
сos a/8×cos a/4×cos a/2

Приложения:

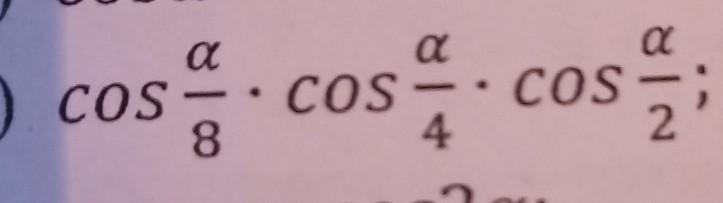
Ответы

Автор ответа: NNNLLL54

Ответ:

Формула синуса двойного угла : $sin2x=2sinx\cdot cosx$ .

Выражение домножим и разделим на $2sin\dfrac{a}{8}$ , чтобы выделить эту формулу .

$\displaystyle cos\frac{a}{8}\cdot cos\frac{a}{4}\cdot cos\frac{a}{2}=\frac{1}{2sin\frac{a}{8}}\cdot \underbrace{2sin\frac{a}{8}\cdot cos\frac{a}{8}}_{sin\frac{a}{4}}\cdot cos\frac{a}{4}\cdot cos\frac{a}{2}=\\\\\\=\frac{1}{2sin\frac{a}{8}}\cdot \underbrace{sin\frac{a}{4}\cdot cos\frac{a}{4}}_{\frac{1}{2}\cdot sin\frac{a}{2}}\cdot cos\frac{a}{2}=\frac{1}{4sin\frac{a}{8}}\cdot \underbrace{sin\frac{a}{2}\cdot cos\frac{a}{2}}_{\frac{1}{2}sina}=\frac{1}{8sin\frac{a}{8}}}\cdot sina=\frac{sina}{8sin\frac{a}{8}}$

engulatovalena: Спасибо огромное!!!

Автор ответа: ZlataSergeeva2000

Решение:

$cos~\dfrac{a}{8} \cdot cos~\dfrac{a}{4} \cdot cos~\dfrac{a}{2} =\dfrac{sin~\dfrac{a}{8} \cdot \Big (cos~\dfrac{a}{8} \cdot cos~\dfrac{a}{4} \cdot cos~\dfrac{a}{2}\Big )}{sin~\dfrac{a}{8} } =$

$=\dfrac{2sin~\dfrac{a}{8} \cdot cos~\dfrac{a}{8} \cdot \Big (cos~\dfrac{a}{4} \cdot cos~\dfrac{a}{2}\Big )}{2sin~\dfrac{a}{8} } =\dfrac{sin~\dfrac{a}{4} \cdot \Big (cos~\dfrac{a}{4} \cdot cos~\dfrac{a}{2}\Big )}{2sin~\dfrac{a}{8} }=$

$\dfrac{2sin~\dfrac{a}{4} \cdot cos~\dfrac{a}{4} \cdot \Big (cos~\dfrac{a}{2}\Big )}{4sin~\dfrac{a}{8} }=\dfrac{sin~\dfrac{a}{2} \cdot cos~\dfrac{a}{2}}{4sin~\dfrac{a}{8} }=\dfrac{2sin~\dfrac{a}{2} \cdot cos~\dfrac{a}{2}}{8sin~\dfrac{a}{8} }=$