В шар радиуса R вписана правильная четырёхугольная призма, сторона основания которой равна a. Найдите площадь боковой поверхности данной призмы​

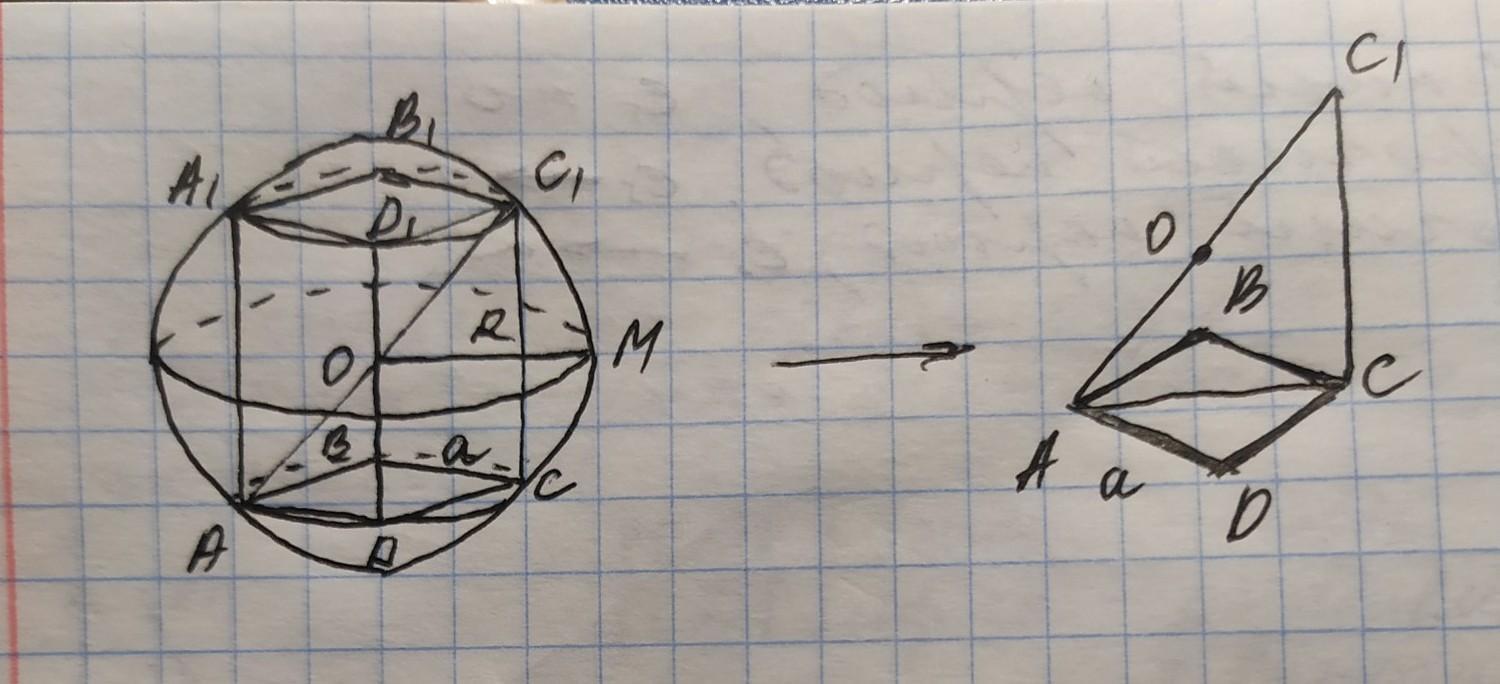
Так как призма вписана в шар, то своими углами она касается шара, и, следовательно, радиус шара будет равен также отрезку, проведенному из центра шара до одного из углов призмы (рисунок прилагается)

Рассмотрим треугольник АСС1, где С1О=ОА как радиусы описанного шара, то есть АС1=2R.

Треугольник прямоугольный, так как призма прямоугольная с высотой СС1. Основание АС равнo АВ√2 (как диагональ квадрата АВСD) = a√2, => по теореме Пифагора можем найти высоту СС1:

√(АС1²-АС²)=√((2R)²-(a√2)²)=√(4R²-2a²), и, как следствие, площадь боковой поверхности:

Sбок=Росн•h=4a•CC1=4a√(4R²-a²)