Предмет: Алгебра,
автор: ao8775733
СРОЧНО , АЛГЕБРА 11 КЛАСС.
Приложения:
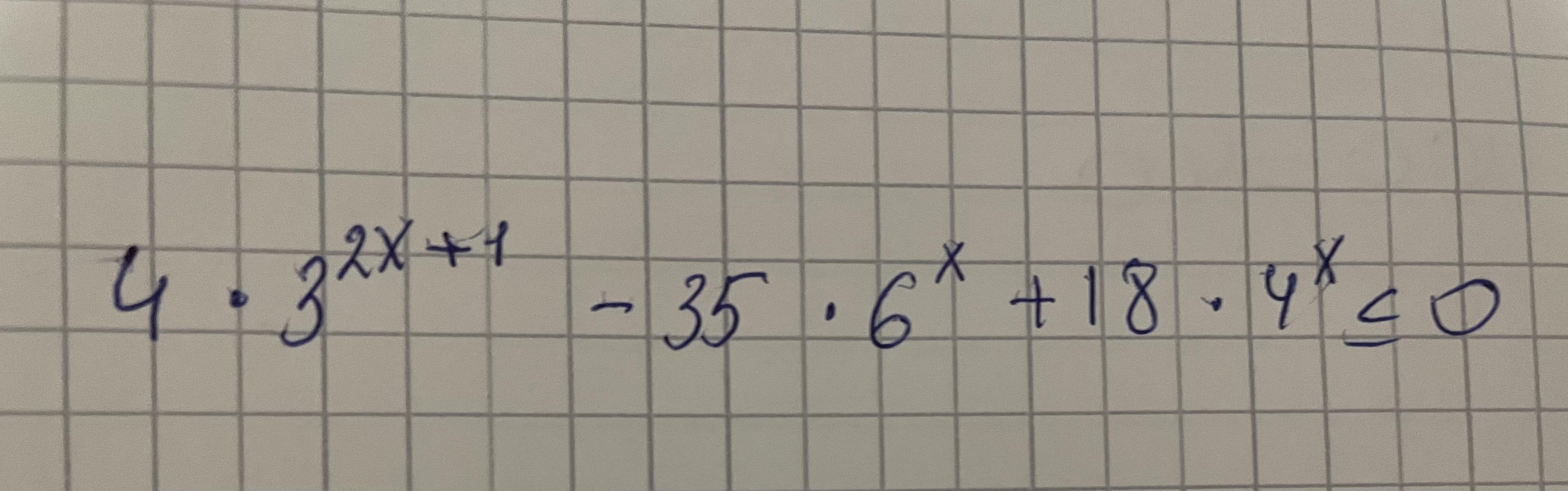
Ответы
Автор ответа:
0
Ответ: [-1;2]
Объяснение: детали во вложении
Приложения:

Автор ответа:
0
Ответ:
Интересные вопросы
Предмет: Русский язык,
автор: коля449
Предмет: Українська мова,
автор: onichenko57
Предмет: Английский язык,
автор: got17
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: vivavova5