Помогите пожалуйста, и по быстрее .
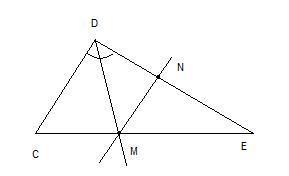
Отрезок ДМ - биссектриса треугольника СДЕ. Через точку М проведена прямая, параллельная стороне СД и пересекающая сто рону ДЕ в точке N. Найдите углы треугольника ДМN. если <СДЕ=68⁰.

1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то <MNE = <CDE = 68°2. Зная, что развернутый угол равен 180°, находим угол DNM:<DNM = 180 - <MNE = 180 - 68 = 112°3. Поскольку DM - биссектриса, то угол MDN = <CDE : 2 = 68 : 2 = 34°4. Зная два угла треугольника DMN, находим неизвестный угол:<DMN = 180 - <MDN - <DNM = 180 - 34 - 112 = 34°