Предмет: Алгебра, автор: miklitr

Решите систему уравнений:

Приложения:

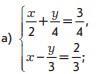
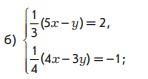
Ответы

Автор ответа: daraprelj

а) $\displaystyle \left \{ {{\frac{x}{2}+\frac{y}{4}=\frac{3}{4} |*4 } \atop {x-\frac{y}{3}=\frac{2}{3} |*3 }} \right.$

⁺ $\displaystyle \left \{ {{2x+y=3} \atop {3x-y=2}} \right.$

$\displaystyle 2x+3x=3+2$

$\displaystyle 5x=5$

$\displaystyle x = 1$

$\displaystyle 2*1+y=3$

$\displaystyle y=3-2$

$\displaystyle y=1$

Ответ: х=1, у=1
б) $\displaystyle \left \{ {{\frac{1}{3}(5x-y)=2|*3 } \atop {\frac{1}{4}(4x-3y)=-1|*4 }} \right.$

$\displaystyle \left \{ {{5x-y=6} \atop {4x-3y=-4}} \right.$

$\displaystyle \left \{ {{y=5x-6} \atop {4x-3*(5x-6)=-4}} \right.$

4x-15x+18 = -4
-11x = -4-18
-11x = -22 |:(-11)
x = 2
y = 5*2-6
y = 4

Ответ: х =2, у = 4

Интересные вопросы

Предмет: Русский язык, автор: glddlsl09

2 года назад

Предмет: Окружающий мир, автор: Пчшаяечзочч

2 года назад

Предмет: Русский язык, автор: лада20061

2 года назад

Предмет: ОБЖ, автор: OksiDemon

8 лет назад

Предмет: Математика, автор: vikashi2017

8 лет назад