Предмет: Алгебра, автор: svorsin13

СРОЧНО. ДАЮ 50 БАЛЛОВ! Форма ответа на фото (можно без решения)

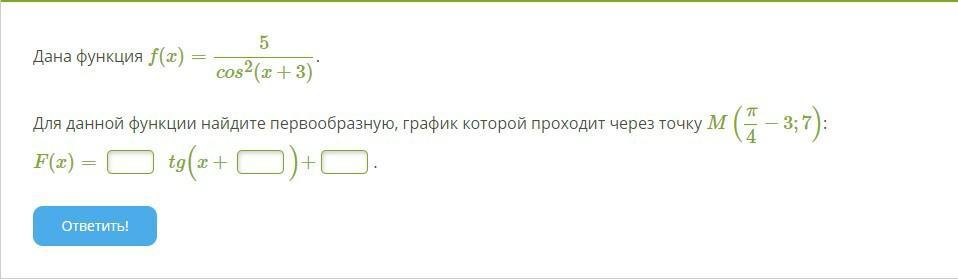
Дана функция f(x)=5/(cos^2)(x+3).

Для данной функции найдите первообразную, график которой проходит через точку M(π/4−3;7):

Приложения:

Ответы

Автор ответа: NNNLLL54

0

Ответ:

Для функции f(x) найдём первообразную F(x) , проходящую через точку $M\Big(\dfrac{\pi}{4}-3;\, 7\ \Big)$ .

$\displaystyle f(x)=3x^2+x\ \ ,\ \ \ F(x)=\int f(x)\, dx+C\\\\F(x)=\int \frac{5\, dx}{cos^2(x+3)}=5\, tg(x+3)+C\\\\\\M\Big(\, \frac{\pi}{4}-3\, ;\, 7\, \Big)\ \ \Rightarrow \ \ \ F\Big(\frac{\pi}{4}-3\Big)=7\\\\F\Big(\frac{\pi}{4}-3\Big)=5\, tg\Big(\frac{\pi}{4}\Big)+C=7\ \ ,\ \ 5\cdot 1+C=7\ ,\ \ \ C=2\\\\\\Otvet:\ \ F(x)\Big|_{M}=5\, tg(x+3)+2\ .\\\\\\\star \int \frac{dx}{cos^2(kx+b)}=\frac{1}{k}\, tg(kx+b)+C\ \ \star$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: Эльчик2005

Что такое искусство?Плиз быстрее!

2 года назад

Предмет: Қазақ тiлi, автор: неизвест

СРОЧНО!!!
Здравствуйте, напишите пожалуйста примеры на Салт етістік и Сабақты етістік.
. И что бы были слова биыл, күздігүні, алғы сөз,баспасөз, Ақтөбе,алдаркөсе.Заранее спасибо

2 года назад

Предмет: Русский язык, автор: Аноним

ехидна - 6 букв, 7 звуков.
Лиса - 4 буквы, 4 звука
Медведь - 7 букв, 6 звуков.
Ястреб - 6 букв, 7 звуков.
Юрок - 4 буквы, 5 звуков.
Ерш - 3 буквы, 4 звука.
Заяц - 4 буквы, 5 звуко

2 года назад

Предмет: Физика, автор: pefedorov11

Сделайте пожалуйста, дам много баллов.
1. Выразить в метрах: а) 3кю; б) 350см; в) 1,5дм
2. Какая скорость больше: 18км/ч и 20м/
3. Тело при равномерном движении за 15с прошло путь 300м. С какой скоростью двигалось тело?

8 лет назад

Предмет: Информатика, автор: mix89098000496

Дано вещественное число с двумя цифрами в целой части и одной цифрой в дробной части. Получить вещественное число, запись которого являлась бы зеркальным отображением исходного числа (например, 36.2 и 2.63).

8 лет назад