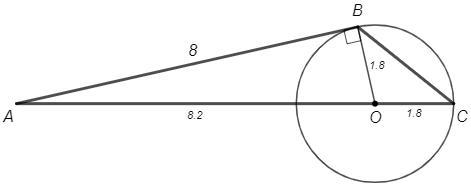
Окружность с центром на стороне AC треугольника ABC проходит через вершину С и касается прямой AB в точке В. Найдите AB, если AC = 10, радиус окружности равен 1,8. ​

O - центр окружности, O∈AC

Радиус соединяет центр с точкой на окружности.

Точка C на окружности, OC - радиус, OC=1,8

AO=AC-OC =10-1,8 =8,2

AB - касательная, B - точка касания.

Радиус в точку касания перпендикулярен касательной.

OB=1,8 (радиус), OB⊥AB, ∠ABO=90°

△ABO, теорема Пифагора:

AB =√(AO^2-OB^2) =√(8,2^2 -1,8^2) =8