Предмет: Геометрия, автор: Аноним

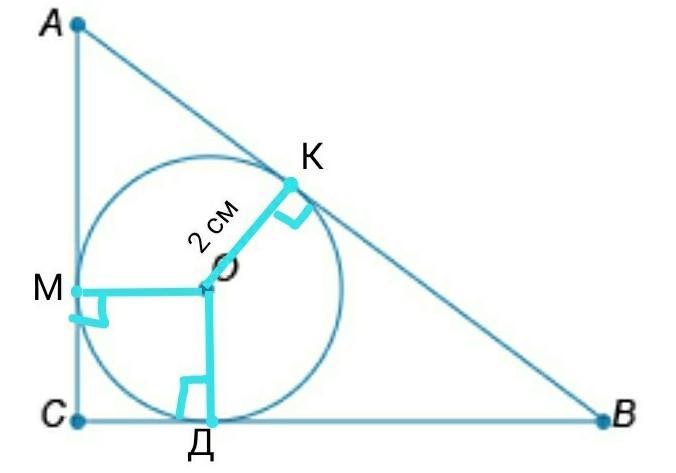
Завдання на фото! ГЕОМЕТРІЯ

Приложения:

Ответы

Автор ответа: Iife20

Ответ:

АС=6см

АВ=10см

ВС=8см

Объяснение:

ДАНО: ∆АВС – прямоугольный, ∠С=90°; вписанная окружность с центром в точке О; К – точка касания; радиус=2см; ВК–АК=2см

НАЙТИ: АВ; АС; ВС

=======================================

Стороны треугольника являются касательными к вписанной окружности. Обозначим точки касания Д и М, соединим О и М, О и Д. ОК, ОД и ОМ – радиусы. Касательная к окружности перпендикулярна радиусу, проведенному в точку касания, поэтому ОК⏊АВ, ОМ ⏊ АС и ОД ⏊ ВС. При этом ∠С – прямой, поэтому четырехугольник МОДС – прямоугольник. Так как МО=ОД=2см, то МО=ОД=СД=СМ=2см → МОДС – квадрат. Пусть АК=х, тогда ВК=х+2. Отрезки касательных, соединяясь в одной точке равны от вершины до точки касания, поэтому:

АМ=АК=х, ВК=ВД=х+2, СМ=СД=2см. Тогда:

АС=2+х, АВ=х+х+2=2х+2, ВС=2+х+2=х+4

АС=2+х

АВ=2х+2

ВС=х+4

Составим уравнение, используя теорему Пифагора:

АС²+ВС²=АВ²

(2х+2)²=(2+х)²+(х+4)²

4х²+8х+4=4+4х+х²+х²+8х+16

4х²+8х+4=2х²+12х+20

4х²+8х–2х²–12х–20+4=0

2х²–4х–16=0

a=2, b= –4; c= –16

Д=b²–4ac=(–4)²–4•2•(–16)=16+128=144=12²

$\\ \\ x1 = \frac{ - b + \sqrt{d} }{2a} = \frac{ 4 + \sqrt{12 {}^{2} } }{2 \times 2} = \\ \\ = \frac{4 + 12}{4} = \frac{16}{4} = 4 \\ \\ x2 = \frac{ - b - \sqrt{12 {}^{2} } }{2a} = \frac{4 - 12}{2 \times 2} = \frac{ - 8}{4} = \\ \\ = - 2$