Предмет: Геометрия,
автор: dhajrtdinov0
Угол между диаметром AB и хордой AC равен 30°. Через точку с проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник ACD равнобедренный.
Ответы
Автор ответа:
1
Дано:
Окр. (О;R)
AB=2R
∠CAB=30°
CD⌒AB=D
Доказать:
△ACD – равнобед.
Доказательство:
1) AD=OC=R, следовательно △AOC – равнобед.
∠C=∠A=30°
2) OC⊥ CD, следовательно ∠ACD=∠OCA+∠DCO
∠ACD=30°+90°=120°
3) △ACD: ∠ D+∠A+∠C=180°
∠D=30°+120°180°, ∠D=30°
∠A=∠D=30°, следовательно AC=CD
Ответ:
△ACD – равнобед.
Приложения:
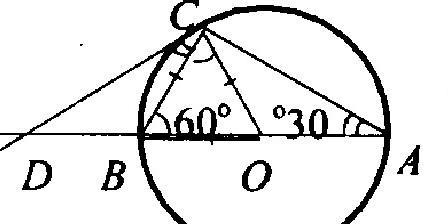
Интересные вопросы
Предмет: Английский язык,
автор: Анюта20045
Предмет: Английский язык,
автор: sasha1145
Предмет: Окружающий мир,
автор: timursgamer
Предмет: Алгебра,
автор: Аноним
Предмет: Химия,
автор: Luorpi