Предмет: Математика, автор: lalkonatala5

помогите решить пожалуйста

Приложения:

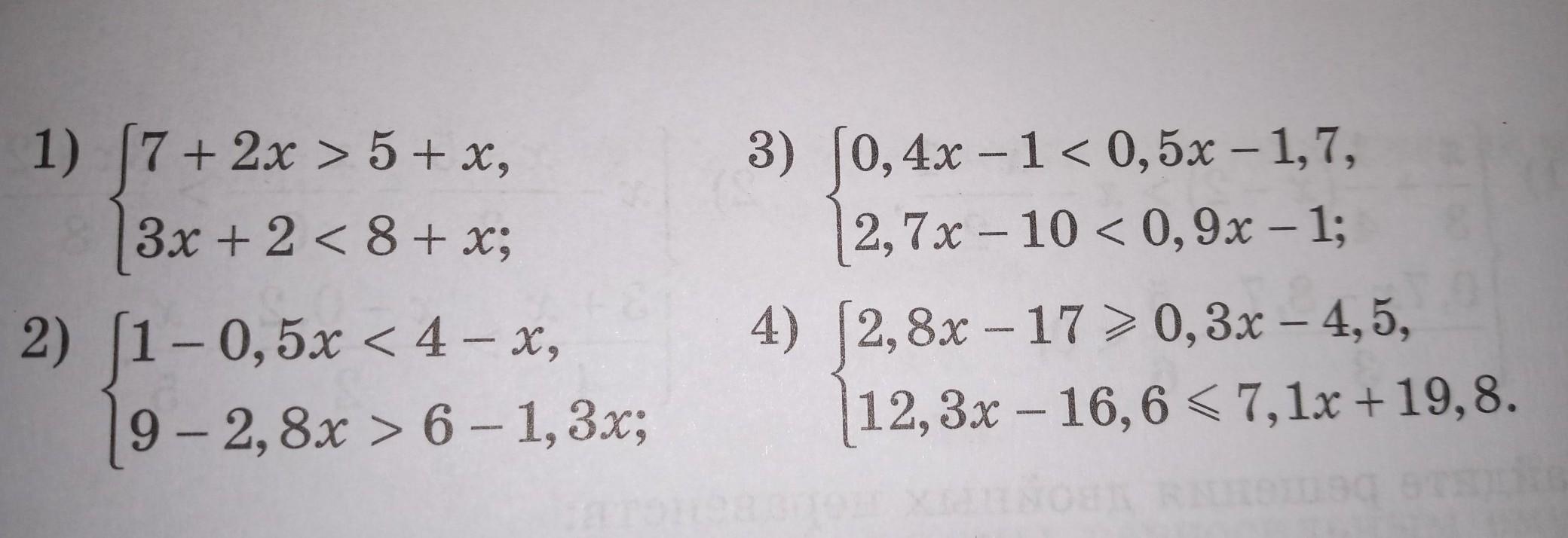
Ответы

Автор ответа: natalyabryukhova

Ответ:

Системы неравенств.

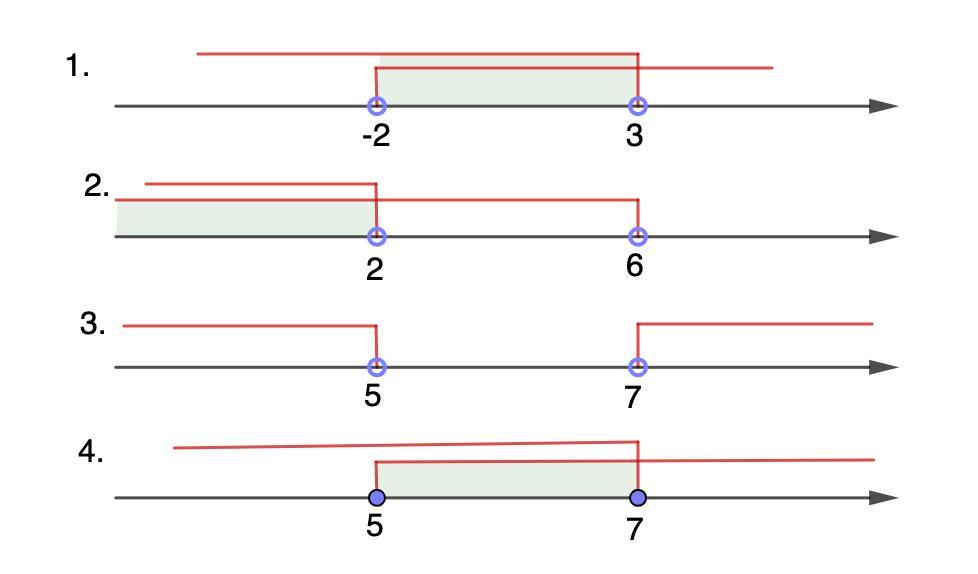
1. x ∈ (-2; 3)

2. x ∈ (-∞; 2)

3. x ∈ ∅

4. x ∈ [5; 7]

Пошаговое объяснение:

Требуется решить системы неравенств.

$\displaystyle \left \{ {{7+2x>5+x} \atop {3x+2<8+x}} \right.$

Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный, приведем подобные члены:

$\displaystyle \left \{ {{2x-x>5-7} \atop {3x-x<8-2}} \right. \iff\left \{ {{x>-2} \;\;\;\;\;\;\;\atop {2x<6}\;\;\;|:2} \right. \iff\left \{ {{x>-2} \atop {x<3}} \right.$

x ∈ (-2; 3)

$\displaystyle \left \{ {{1-0,5x<4-x} \atop {9-2,8x>6-1,3x}} \right.$

Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный, приведем подобные члены:

$\displaystyle \left \{ {{-0,5x+x<4-1} \atop {-2,8x+1,3x>6-9}} \right. \iff\left \{ {{0,5x<3} \;\;\;|:0,5\atop {-1,5x>-3}\;\;\;|:(-1,5)} \right.$

Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.

$\displaystyle \left \{ {{x<6} \atop {x<2}} \right.$

x ∈ (-∞; 2)

$\displaystyle \left \{ {{0,4x-1<0,5x-1,7} \atop {2,7x-10<0,9x-1}} \right.$

Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный, приведем подобные члены:

$\displaystyle \left \{ {{0,4x-0,5x<-1,7+1} \atop {2,7x-0,9x<-1+10}} \right. \iff\left \{ {{-0,1x<-0,7\;\;\;|:(-0,1)} \atop {1,8x<9\;\;\;\;\;\;\;\;\;\;|:1,8\;\;\;}} \right.$

В первом неравенстве не забываем перевернуть знак неравенства:

$\displaystyle \left \{ {{x>7} \atop {x<5}} \right.$

x ∈ ∅

$\displaystyle \left \{ {{2,8x-17\geq 0,3x-4,5} \atop {12,3x-16,6\leq 7,1x+19,8}} \right.$

Перенесем неизвестные влево, известные вправо, поменяв знак на противоположный, приведем подобные члены:

$\displaystyle \left \{ {{2,8x-0,3x\geq -4,5+17} \atop {12,3x-7,1x\leq 19,8+16,6}} \right. \iff\left \{ {{2,5x\geq 12,5\;\;\;|:2,5} \atop {5,2x\leq 36,4\;\;\;|:5,2}} \right. \iff\\\\\left \{ {{x\geq 5} \atop {x\leq 7}} \right.$