периметр ромба 48под корнем 2см2 площадь ромба равна 144 под корнем 2 см2 найти углы между сторонами ромба ​

Ответ:

45°, 135°, 45°, 135° - углы ромба.

Объяснение:

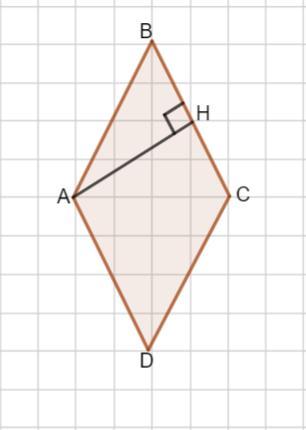
Пусть задан ромб АВСD

Периметр ромба равен 48√2 см. Так как у ромба все стороны равны, то найдем сторону ромба

Значит, сторона ромба равна 12√2 см.

см.

По условию площадь ромба равна 144√2 см².

Площадь ромба равна произведению стороны на высоту, проведенную к стороне.

Пусть АН - высота ромба

см.

Рассмотрим Δ АВН - прямоугольный. В нем известны гипотенуза АВ  и противолежащий к ∠ А катет АН.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Тогда ∠ А= 45 °. У ромба противолежащие углы равны.

Значит, ∠ D=∠A= 45°.

Так как ∠ А и ∠В - внутренние односторонние, образованные

ВС ║АD и секущей АВ  . Сумма односторонних углов равна 180°

∠В =180 °- 45°=135°.

∠С=∠В=135°.