Решите прямоугольный треугольник, если высота равна 4, а одна из проекций катета равна 3
С рисунком
ДАЮ 50 БАЛЛОВ
Ответы
Ответ: AC=5;
AB=8,3(3)
BC=6,6(6
Угол А=arсsin 0,8≈53,13°
Угол В=arсsin 0,6 ≈36,87
Объяснение:
Решение треугольника − это нахождение всех его элементов (трех сторон и трех углов) по известным элементам.
——
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
∆ АВС~∆ АСН
Угол А - общий, угол АВС=углу АСН
По т.Пифагора
катет АС²=СН²+АН², откуда АС=√(4²+3²)=5
(заметим отношение сторон в ∆ АСВ - 3:4:5, этот треугольник «египетский»)
sin(A)=CH:AC=4/5=0,8
Угол А=arсsin 0,8≈53,13 °
sin(B)=sin(ACH)=AH:AC=3/5=0,6
Угол В=arсsin 0,6 ≈36,87 °( или из суммы острых углов прямоугольного треугольника 90°-<А=90°-53,13°)
АВ=АС:sin<B=5/0,6=8,3(3)
ВС=АВ•sin(A)=8,3(3)•0,8=6,6(6)
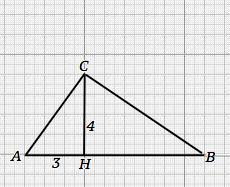
СН=4 см , ВН=3 см. Найти АС.АВ.
ΔСНВ , по Пифагору СВ=√(3²+4²)=5
Тк СВ²=АВ*НВ ⇒ 5²=АВ*3 , АВ=25/3 .
ТогдаАН=25/3-3=25/3-9/3=16/3.
ΔАВС по Пифагору ,АС=√( (25/3)²-5²)=.....ой долго считать .Считай сам