СРОЧНО 28 БАЛЛОВ!!!

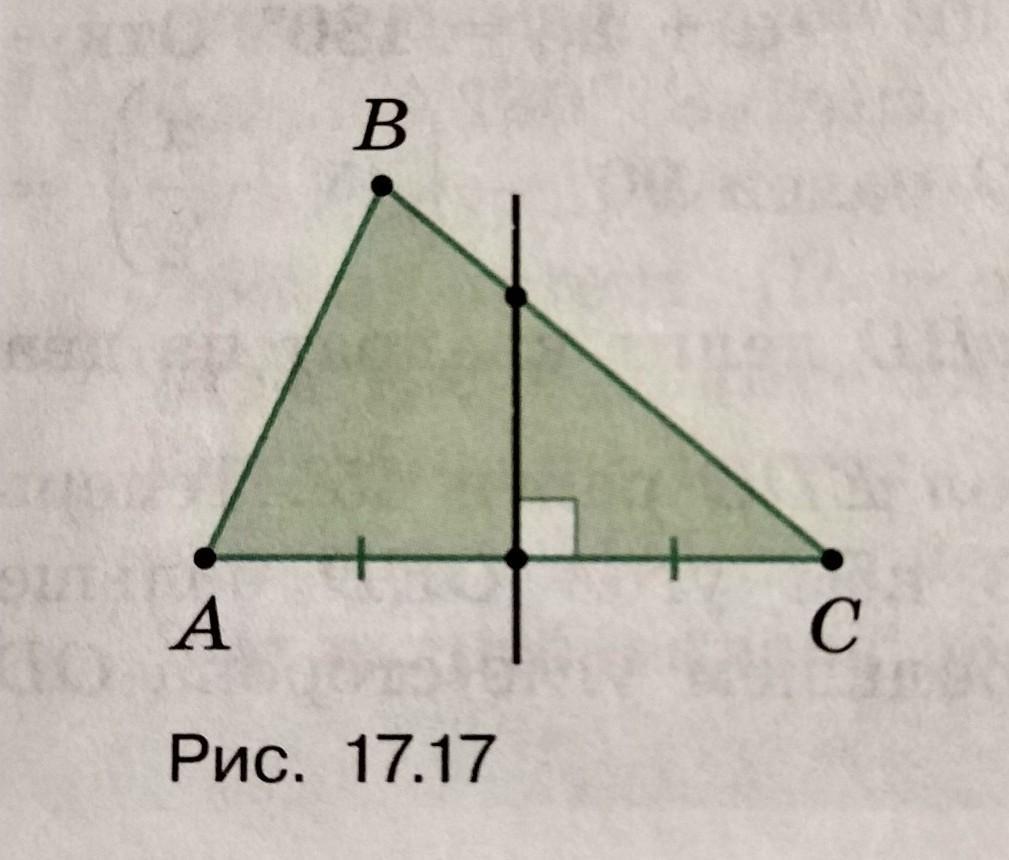
Серединный перпендикуляр к стороне AC треугольника ABC пересекает его сторону BC. Докажите, что ВС > AB (рис. 17.17).​

Ответ:

Объяснение:

Чтобы доказать что ВС > AB, нужно доказать что ∠А > ∠C (против большего угла лежит большая сторона);

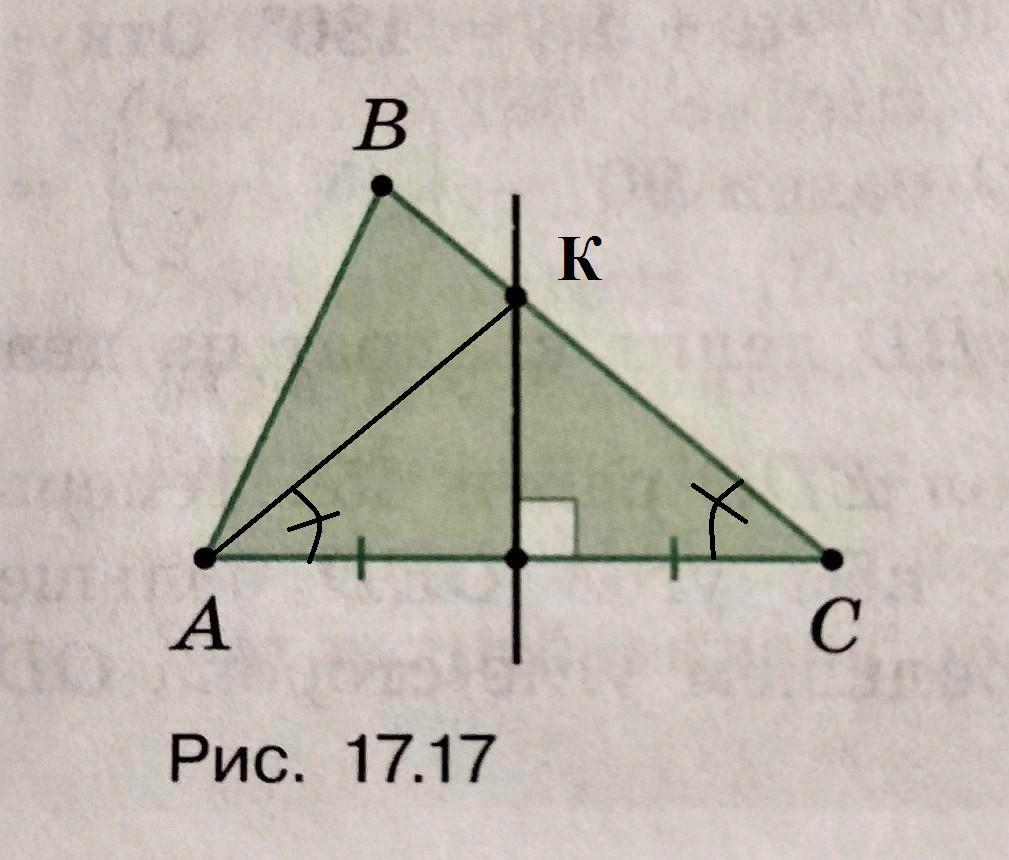
обозначим точку пересечения серединного перпендикуляра со стороной ВС - К, проведем АК, ΔАКС равнобедренный, АК=КС ⇒ ∠А=∠С;

в ΔАВС ∠А=∠С+∠КАВ ⇒ ∠А > ∠C следовательно ВС > AB.