Предмет: Алгебра, автор: 123038387

9 КЛАСС!СРОЧНО!!!!! Помогите пожалуйста,прошу. ДАЮ 70 БАЛЛОВ!! Только 1 и 2 задание!!

Приложения:

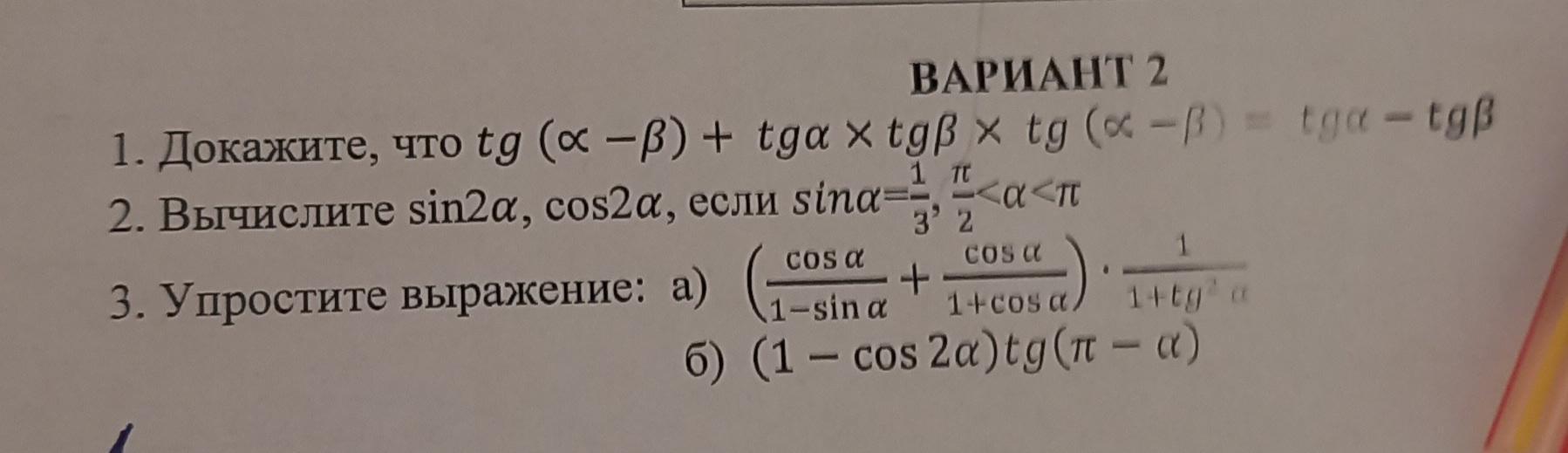
Аноним: Щя, поищю

Ответы

Автор ответа: Alnadya

1

Решение.

$\bf 1.\ \ \underline{tg(a-\beta )}+tga\cdot tg\beta \cdot \underline{tg(a-\beta )}=\underline{tg(a-\beta )}\cdot \Big(1+tga\cdot tg\beta \Big)=\\\\\\=\dfrac{tga-tg\beta }{1+tga\cdot tg\beta }\cdot (1+tga\cdot tg\beta )=tga-tg\beta \\\\\\tga-tg\beta =tga-tg\beta$

Применили формулу тангенса разности .

$\bf 2.\ \ sina=\dfrac{1}{3}\\\\sin^2a+cos^2a=1\ \ \Rightarrow \ \ \ cos^2a=1-sin^2a=1-\dfrac{1}{9}=\dfrac{8}{9}$

Угол лежит во 2 четверти, значит $\bf cosa < 0$ и $\bf cosa=-\dfrac{2\sqrt2}{3}$ .

$\bf sin2a=2\cdot sina\cdot cosa=2\cdot \dfrac{1}{3}\cdot \dfrac{-2\sqrt2}{3}=-\dfrac{4\sqrt2}{9}\\\\\\cos2a=1-2sin^2a=1-2\cdot \dfrac{1}{9}=\dfrac{7}{9}$

3.

$\displaystyle \bf a.\ \ \Big(\frac{cosa}{1-sina}+\frac{cosa}{1+sina}\Big)\cdot \frac{1}{\, 1+tg^2a}=\\\\\\=\frac{cosa+sina\cdot cosa+cosa-sina\cdot cosa}{(1-sina)(a+sina)}\, \cdot \, cos^2a=\frac{2\cdot cosa}{1-sin^2a}\cdot cos^2a=\\\\\\=\frac{2\cdot cos^3a}{cos^2a}=2\cdot cosa$

Применили основное тригонометрическое тождество:

$\bf sin^2a+cos^2a=1\ \ \Rightarrow \ \ cos^2a=1-sin^2a$ и $\bf 1+tg^2a=\dfrac{1}{cos^2a}$ .

$\displaystyle \bf b.\ \ (1-cos2a)\cdot tg\Big(\pi -a\Big)=$

Применим формулы приведения и косинуса двойного угла.

$\bf =\Big(1-(1-2sin^2a)\Big)\cdot \Big(-tga\Big)=2sin^2a\cdot \dfrac{-sina}{cosa}=-\dfrac{2\cdot sin^3a}{ cosa}$

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: ivan13123

между концами рубиновой звезды видны звенья якорной цепи, из-под которых выступают пучки расходящихся лучей. Где здесь причастия и надо сделать морфологический разбор этого причастия или их. Пж Надо.Даю много балов!!!

2 года назад

Предмет: Английский язык, автор: еллвлс

Сделать номера 7,8,9 тоесть все

2 года назад

Предмет: Русский язык, автор: Typaya11

Помогите пожалуйста найти одно лишнее слово в каждой строке и объяснить почему оно лишнее

2 года назад

Предмет: Другие предметы, автор: Аноним

интересные факты про Дали

8 лет назад

Предмет: Алгебра, автор: trifonovamaria1

Помогите пожалуйста!!
решите уравнение (1/3)^2x=8x;
(1/4)^x=(1/5)^x

8 лет назад