Предмет: Математика,
автор: zeryofficial
Помогите решить задачу по геометрии
Приложения:
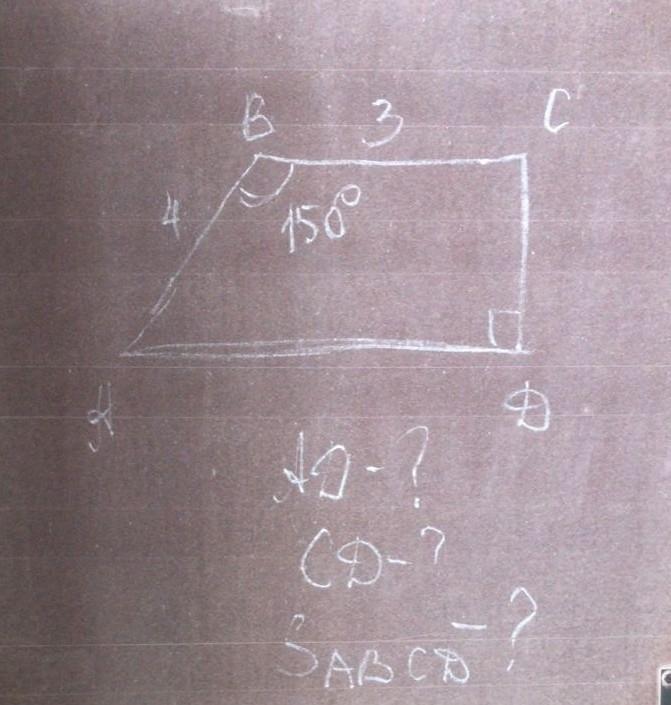
Ответы
Автор ответа:
1
Пошаговое объяснение:
1) проведём ВН перпендикулярно AD, тогда BCDH — прямоугольник(т.к. CD перпендикулярно BC и BH перпендикулярно AD, BC || HD, BH || CD), в котором по его св-ву BC = HD = 3 и BH = CD.
2) угол АВН = 150° - угол НВС
угол АВН = 150° - 90° = 60°
3) т.к. ВН перпендикулярно AD, то треугольник АВН — прямоугольный, следовательно:
sin АВН = АН/АВ
sin 60° = АН/4
cos ABH = BH/AB
cos 60° = BH/4
4) ВН = CD = 2, а АD = AH+HD = 2√3+3
5)
если вам понравился мой ответ можете поставить пометку «Лучший ответ»?
Интересные вопросы
Предмет: Українська література,
автор: MilenaMusienko
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: ЮлияСемушина
Предмет: Химия,
автор: krot2370
Предмет: Математика,
автор: sasha1836