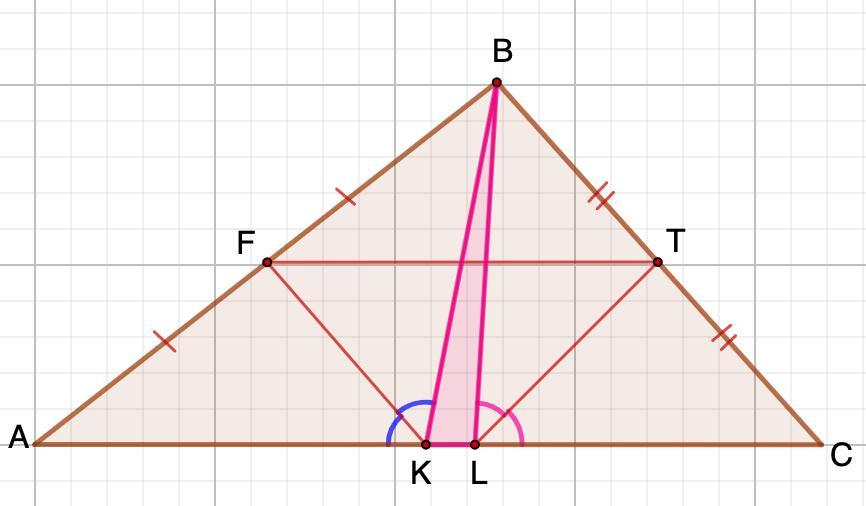
Точки F и T - середины сторон AB и BC треугольника ABC соответственно. Точки K и L лежат на стороне AC, причём K лежит между A и L. Известно, что /_AKF = /_BKF, /_CLT = /_BLT, FT=36. Найдите периметр треугольника BKL.

Ответ:

Периметр треугольника BKL равен 72 ед.

Объяснение:

Требуется найти периметр треугольника BKL.

Дано: ΔАВС.

AF = FB; BT = TC;

∠AKF =∠BKF, ∠CLT = ∠BLT,

FT=36.

Найти: Р(BKL)

Решение:

1. Рассмотрим ΔАКВ.

AF = FB ⇒ KF - медиана.

∠AKF =∠BKF ⇒  KF  - биссектриса.

• Если в треугольнике медиана является биссектрисой, то этот треугольник равнобедренный.

⇒ ΔАКВ - равнобедренный.

АК = КВ.

2. Рассмотрим ΔBLC.

BT = TC ⇒ LT - медиана.

∠CLT = ∠BLT ⇒  LT  - биссектриса.

⇒ ΔBLC - равнобедренный.

BL = LC

3. Найдем периметр Δ BKL.

• Периметр - сумма длин всех сторон треугольника.

Р(BKL) = KB + KL + BL

АК = КВ

BL = LC

Р(BKL) = АК + KL +LC = AC

FT - средняя линия ΔАВС.

• Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и равна половине этой стороны.

⇒ АС = 2FT = 36 · 2 = 72

Р(BKL)  = AC = 72 ед.