найдите площадь боковой поверхности правильной треугольной пирамиды, сторона основания которой рана 24, а боковое ребро равно 15.
полное решение

Ответ:

Площадь боковой поверхности пирамиды равна 324 кв. ед.

Объяснение:

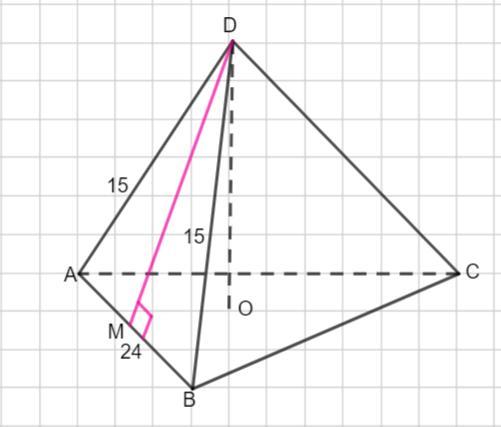
По условию задана правильная треугольная пирамида ABCD.

Площадь боковой поверхности правильной пирамиды равна полупроизведению периметра основания на апофему .

сторона треугольника

Проведем высоту боковой грани DM . Это и будет апофема .

ΔADВ - равнобедренный, поэтому высота, проведенная к основанию является медианой .

Тогда АМ=МВ =24:2=12

Δ AMD - прямоугольный . Найдем апофему DM по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Значит, апофема равна 9.

Найдем площадь боковой поверхности пирамиды

Площадь боковой поверхности пирамиды равна 324 кв. ед.