Предмет: Математика, автор: wainettyan

Нужно найти предел последовательности! Помогите пожалуйста! Очень срочно!

Приложения:

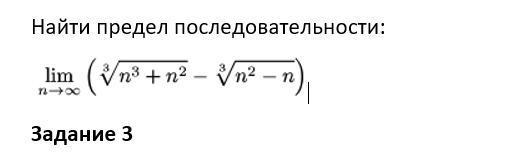
Ответы

Автор ответа: yugolovin

Ответ: $\infty.$

Пошаговое объяснение: ${}$

$\lim\limits_{n\to \infty}\left(\sqrt[3]{n^3+n^2}-\sqrt[3]{n^2-n}\right)=\lim\limits_{n\to \infty}n\left(\sqrt[3]{1+\frac{1}{n}}-\sqrt[3]{\frac{1}{n}-\frac{1}{n^2}}\right)=\infty(1-0)=\infty.$

Мы воспользовались тем, что $\lim\limits_{n\to \infty}\dfrac{1}{n}=0.$

wainettyan: Огромное спасибо Вам!!

yugolovin: ))

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Українська мова, автор: Аноним

Складіть і запишіть речення зі словами здається, може, видно так, щоб в одному з речень вони були вставними, а в іншому - членами речення

2 года назад

Предмет: Английский язык, автор: пщшпггпо

как по английски написать тумбочка с транскрипцией

2 года назад

Предмет: Другие предметы, автор: KlAsSnYy

Приведите примеры об открытиях в искусстве, подтвержденных современной наукой, даю 30 б

2 года назад

Предмет: Математика, автор: nastyashygailenko555

Під час сушіння сливи втрачають 76% своєї маси. Визначте, скільки свіжих слив треба взяти, щоб отримати 18 кг сушених.

8 лет назад

Предмет: Қазақ тiлi, автор: WolfDemon

Табиғат,тау,дала сөздерін қатыстырып,төрт жол өлең құраңдар помогите пожалуйста

8 лет назад