Предмет: Алгебра, автор: Reideen

Задание приложено...

Приложения:

Аноним: Здравствуйте вы не могли бы вы мне помочь с химией пожалуйста умоляю

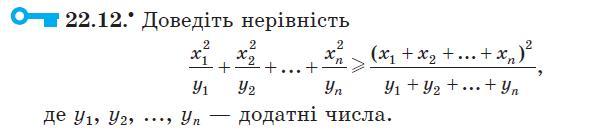
Ответы

Автор ответа: mathkot

Ответ:

Метод математической индукции:

Для того, чтобы доказать, что некоторое утверждение верно при натуральном $n$ необходимо выполнить следующие условия:

База индукции:

1) Доказать, что утверждение верно при $n = 1$

Индуктивный переход:

2) Сделать гипотезу, что утверждение верно для $n = k$ и на основании данной гипотезы доказать, что утверждение верно для $n = k + 1$

Если выполнены утверждения 1) и 2), то исходное утверждение доказано для всех натуральных $n$ методом математической индукции.

Воспользуемся методом математиечской индукции для доказательства неравенства:

$\displaystyle \frac{x_{1}^{2}}{y_{1}} + \frac{x_{2}^{2}}{y_{2}} + \ldots + \frac{x_{n}^{2}}{y_{n}} \geq \frac{(x_{1} + x_{2} + \ldots + x_{n})^{2}}{y_{1} + y_{2} + \ldots + y_{n}}$

$y_{1}, y_{2}, \ ...,y_{n} > 0$

База индукции:

$n = 1; \displaystyle \frac{x_{1}^{2}}{y_{1}} = \displaystyle \frac{x_{1}^{2}}{y_{1}}$ - верно

$n = 2;$

$\boxed{\displaystyle \frac{x_{1}^{2}}{y_{1}} + \frac{x_{2}^{2}}{y_{2}} \geq \frac{(x_{1} + x_{2})^{2}}{y_{1} + y_{2}}}$ - (*) верно

$\displaystyle \frac{x_{1}^{2}y_{2} + x_{2}^{2}y_{1}}{y_{1}y_{2}} \geq \frac{x_{1}^{2} + 2x_{1}x_{2} + x_{2}^{2}}{y_{1} + y_{2}} \bigg |\cdot y_{1} y_{2}(y_{1} + y_{2})$

$(y_{1} + y_{2})(x_{1}^{2}y_{2} + x_{2}^{2}y_{1}) \geq y_{1} y_{2}(x_{1}^{2} + 2x_{1}x_{2} + x_{2}^{2})$

$x_{1}^{2}y_{1}y_{2} + x_{2}^{2}y_{1}^{2} + x_{1}^{2}y_{2}^{2} + x_{2}^{2}y_{1}y_{2} \geq y_{1} y_{2}x_{1}^{2} + 2x_{1}x_{2}y_{1} y_{2} + y_{1} y_{2}x_{2}^{2}$

$x_{2}^{2}y_{1}^{2} + x_{1}^{2}y_{2}^{2} \geq 2x_{1}x_{2}y_{1} y_{2}$

$x_{2}^{2}y_{1}^{2} - 2x_{1}x_{2}y_{1} y_{2} + x_{1}^{2}y_{2}^{2} \geq 0$

$(x_{2}y_{1} - x_{1}y_{2})^{2} \geq 0$

Индуктивный переход:

$n = k;$

$\displaystyle \frac{x_{1}^{2}}{y_{1}} + \frac{x_{2}^{2}}{y_{2}} + \ldots + \frac{x_{k}^{2}}{y_{k}} \geq \frac{(x_{1} + x_{2} + \ldots + x_{k})^{2}}{y_{1} + y_{2} + \ldots + y_{k}}$

$n = k + 1;$

Чтобы доказать утверждение для $n = k + 1$ воспользуемся неравенство (*), которое является верным.

$\displaystyle \frac{x_{1}^{2}}{y_{1}} + \frac{x_{2}^{2}}{y_{2}} + \ldots + \frac{x_{k}^{2}}{y_{k}} + \frac{x_{k + 1}^{2}}{y_{k + 1}} \geq \frac{(x_{1} + x_{2} + \ldots + x_{k})^{2}}{y_{1} + y_{2} + \ldots + y_{k}} + \frac{x_{k + 1}^{2}}{y_{k + 1}} \geq \frac{(x_{1} + x_{2} + \ldots + x_{k} + x_{k + 1})^{2}}{y_{1} + y_{2} + \ldots + y_{k} + y_{k + 1}}$

То есть неравенство (*) было применено к части $\displaystyle \frac{(x_{1} + x_{2} + \ldots + x_{k})^{2}}{y_{1} + y_{2} + \ldots + y_{k}}$ и к части $\dfrac{x_{k + 1}^{2}}{y_{k + 1}}$ и на основании этого было доказано первоначальное неравенство $\boxed{\displaystyle \frac{x_{1}^{2}}{y_{1}} + \frac{x_{2}^{2}}{y_{2}} + \ldots + \frac{x_{n}^{2}}{y_{n}} \geq \frac{(x_{1} + x_{2} + \ldots + x_{n})^{2}}{y_{1} + y_{2} + \ldots + y_{n}}}$ при условии $y_{1}, y_{2}, \ ...,y_{n} > 0$ .