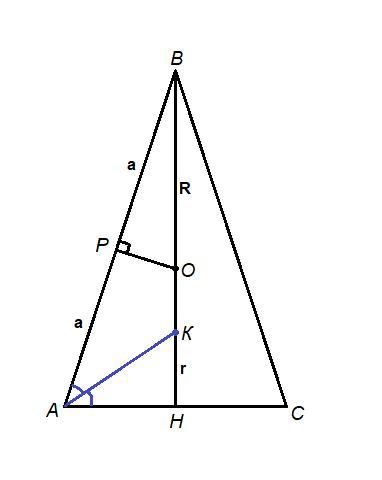
Площа круга, описаного навколо рівнобедреного трикутника, дорів нює 100л см². Знайдіть площу круга, вписаного в цей трикутник, якщо висота, проведена до основи, дорівнює 18 см.
Ответы
Ответ:
Площадь круга, вписанного в треугольник:
Sвп. = (44π - 8√10π) см²
Объяснение:
Площадь описанного круга:
Sоп. = πR²
Sоп. = 100π см²
πR² = 100π
R² = 100
R = 10 см
- Центр описанной около треугольника окружности лежит в точке пересечения серединных перпендикуляров к сторонам треугольника.
ВН = 18 см - высота, проведенная к основанию, значит и медиана и биссектриса, тогда центр описанной окружности, точка О, лежит на ВН.
OB = R = 10 см
Проведем ОР⊥АВ. Так как ОР - серединный перпендикуляр, то Р - середина АВ.
ΔВРО ~ ΔВНА по двум углам:
- ∠ВРО = ∠ВНА = 90°,
- угол при вершине В общий.
a² = 90
a = 3√10 см
АВ = 2а = 6√10 см
Из прямоугольного треугольника АВН по теореме Пифагора:
см
- Центр окружности, вписанной в треугольник, лежит в точке пересечения биссектрис.
Проведем биссектрису угла А. Она пересечет ВН в точке К. К - центр вписанной окружности.
KH = r - радиус вписанной окружности.
- Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Для треугольника АВН:
Площадь вписанного круга:
Sвп. = πr²
Sвп. = π · 4(√10 - 1)² = 4π(10 - 2√10 + 1) = 4π(11 - 2√10)
Sвп. = (44π - 8√10π) см²