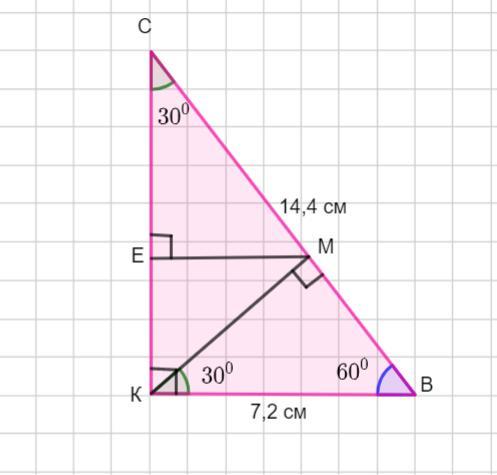
В прямоугольном треугольнике ВКС гипотенуза СВ равна 14,4 см, катет ВК равен 7,2 см, КМ – высота. Найдите расстояние от точки М до прямой КС.
Зарание спасибо

Ответ:

Расстояние от точки М до прямой КС равно 5,4 см.

Объяснение:

По условию  дан Δ ВКС - прямоугольный.

СВ -гипотенуза , СВ =14,4 см. Катет ВК = 7, 2 см.

Так как катет ВС в 2 раза меньше гипотенузы  СВ, то ∠С =30°.

Сумма острых углов прямоугольного треугольника равна 90°,

тогда ∠ В =90°-30° = 60°.

В заданном треугольнике проведена высота КМ.

Рассмотрим Δ КМВ - прямоугольный, так как  КМ- высота.

Если ∠ В= 60°, то ∠ВКМ =30°.

По свойству катета лежащего напротив угла в 30°, катет ВМ равен половине гипотенузы

см

Тогда

cм

По условию надо найти расстояние от точки М до прямой КС. Тогда из точки М опустим перпендикуляр МЕ на сторону КС.

Тогда ΔСЕМ - прямоугольный. Катет МЕ лежит напротив угла в 30° и он равен половине гипотенузы СМ.

МЕ= 10,8:2= 5,4 см.

Тогда расстояние от точки М до прямой КС равно 5,4 см.