СРОЧНО 65 БААЛЛОВ
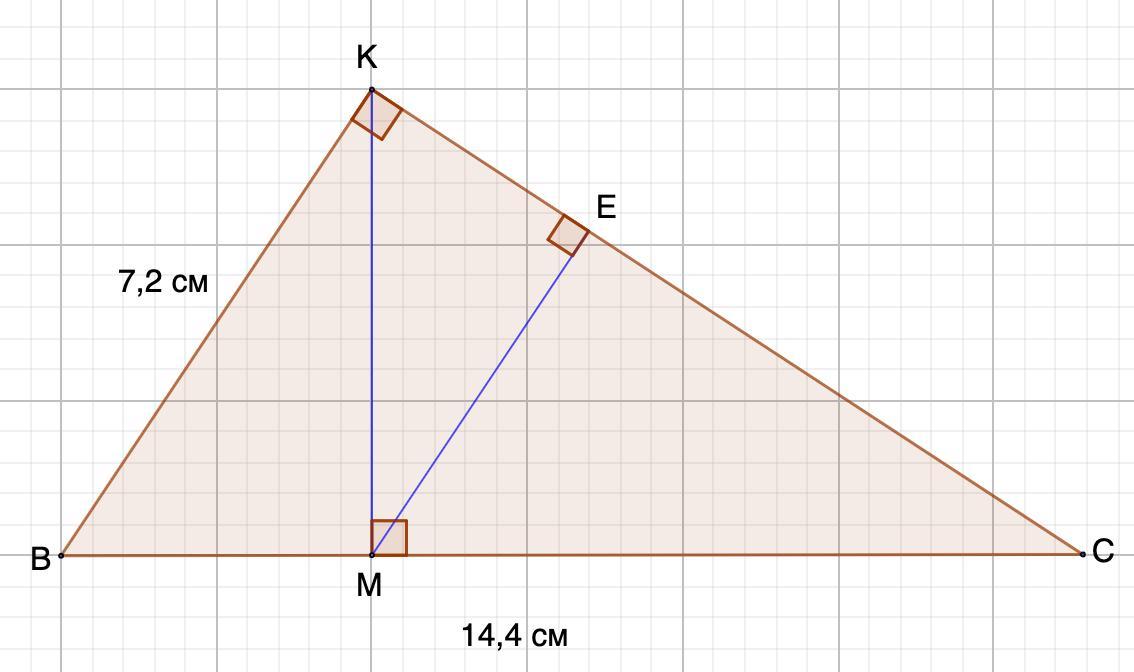
В прямоугольном треугольнике ВКС гипотенуза СВ равна 14,4 см, катет ВК равен 7,2 см, КМ – высота. Найдите расстояние от точки М до прямой КС.

Ответ:

Расстояние от точки М до прямой КС равно 5,4 см.

Объяснение:

Требуется найти расстояние от точки М до прямой КС.

Дано: ΔВКС - прямоугольный;

СВ = 14,4 см - гипотенуза;

ВК = 7,2 см;

КМ - высота;

Найти: расстояние от точки М до прямой КС.

Решение:

1. Рассмотрим ΔВКС.

КМ - высота.

• Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.

⇒ ВК² = ВМ · ВС

7,2² = ВМ · 14,4

ВМ = 51,84 : 14,4

ВМ = 3,6 (см)

⇒ МС = ВС - ВМ = 14,4 - 3,6 = 10,8 (см)

Также заметим, что катет ВС в два раза меньше гипотенузы.

СВ = 2ВК; 14,4 = 7,2 · 2

• Если в прямоугольном треугольнике катет в два раза меньше гипотенузы, то этот катет лежит против угла 30°.

⇒ ∠С = 30°.

2.

• Расстояние от точки до прямой - длина перпендикуляра, опущенного из данной точки на данную прямую.

⇒ МЕ - искомое расстояние.

Рассмотрим ΔМЕС - прямоугольный.

∠С = 30°;

МС = 10,8 см - гипотенуза;

Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒МЕ = МС : 2 = 10,8 : 2 = 5,4 (см)

Расстояние от точки М до прямой КС равно 5,4 см.