Предмет: Математика,
автор: gorosukolga512
Найдите сумму сорока первых членов арифметической прогрессии (аn), если: 1) a7 = 6, а17 = 26.
Найдите сумму двадцати первых членов арифметиче ской прогрессии (an), если:
1) a1 = 7, a11 = 27;
2) a5 = 58, a15 = 16.
Ответы
Автор ответа:
2
1. Выразим седьмой и семнадцатый члены прогрессии через первый член и разность:
а7 = а1 + 6d;
а17 = а1 + 16d.
а1 + 6d = 6;
а1 + 16d = 26.
Вычтем из второго уравнения первое и найдем d:
10d = 20;
d = 20 : 10;
d = 2.
а1 + 2 * 6 = 6;
а1 = 6 — 12 = - 6.
По формуле Sn = (2a1 + d(n — 1)) * n / 2 найдем S40:
S40 = (2 * (- 6) + 2 * (40 — 1)) * 40 / 2 = (- 12 + 78) * 20 = 66 * 20 = 1320.
Ответ: S40 = 1320.
2.2) d=(a15-a5)/(15-5)=(16-58)/10=-4.2
a1=a5-4d=58-4(-4.2)=74.8
S20=20(2*74.8+19*(-4.2))/2=10(149.6-79.8)=698
Пошаговое объяснение:
на фотографии приведено решение задания 2.2)
Приложения:
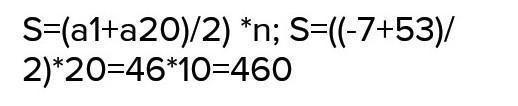
gorosukolga512:
можно просто на каждое задание ответ?
Интересные вопросы
Предмет: Русский язык,
автор: TheEnderGame
Предмет: Русский язык,
автор: Хлопушка11
Предмет: Окружающий мир,
автор: tanyadanko
Предмет: Русский язык,
автор: санти3
Предмет: Математика,
автор: 11queen