Предмет: Алгебра, автор: lizapogorelaia66

ДАЮ 30 баллов;!!!!!!! срочно!!!!!!!!!!!!! решать самим

Приложения:

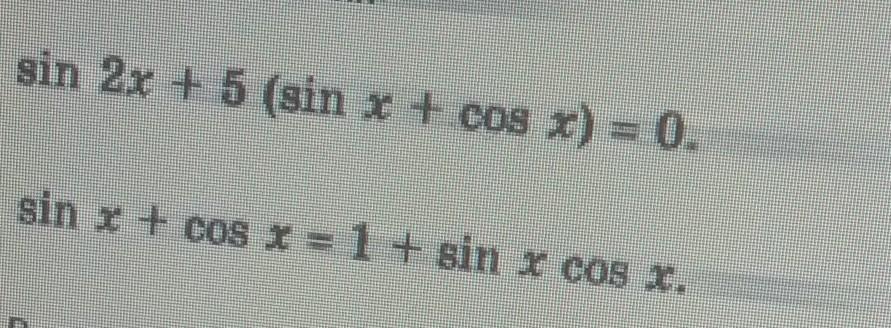
Ответы

Автор ответа: NNNLLL54

Ответ:

$1)\ \ sin2x+5\, (sinx+cosx)=0\\\\2\, sinx\cdot cosx+5\, (sinx+cosx)=0$

Решаем с помощью замены: $t=sinx+cosx$ .

$t^2=sin^2x+2\, sinx\cdot cosx+cos^2x=1+2\, sinx\cdot cosx\ \ \Rightarrow \\\\2\, sinx\cdot cosx=t^2-1$

Теперь подставим в уравнение: $t^2-1+5t=0\ \ ,\ \ t^2+5t-1=0$ .

Решаем квадратное уравнение . $D=5^2-4\cdot (-1)=29\ \ ,$

$t_1=\dfrac{-5-\sqrt{29}}{2}\approx -5,19\ \ ,\ \ \ t_2=\dfrac{-5+\sqrt{29}}{2}\approx 0,19$

$a)\ \ sinx+cosx=\dfrac{-5-\sqrt{29}}{2}\\\\sinx+sin(\dfrac{\pi }{2}-x)=\dfrac{-5-\sqrt{29}}{2}\ \ ,\ \ \ 2sin\dfrac{\pi}{4}\cdot cos(x-\dfrac{\pi}{4})=\dfrac{-5-\sqrt{29}}{2}\\\\\sqrt2\cdot cos(x-\dfrac{\pi}{4})=\dfrac{-5-\sqrt{29}}{2}\ \ ,\ \ \ cos(x-\dfrac{\pi}{4})=\dfrac{-5-\sqrt{29}}{2\sqrt2}\approx -3,71 < -1$

Так как $-1\leq cos(x-\dfrac{\pi}{4})\leq 1$ , то функция косинус не может принимать значение, меньшее -1, поэтому уравнение не имеет решений.

$b)\ \ sinx+cosx=\dfrac{-5+\sqrt{29}}{2}\\\\\sqrt2\cdot cos(x-\dfrac{\pi}{4})=\dfrac{-5+\sqrt{29}}{2}\ \ ,\ \ \ cos(x-\dfrac{\pi}{4})=\dfrac{-5+\sqrt{29}}{2\sqrt2}\approx 0,14\\\\x-\dfrac{\pi}{4}=\pm arccos\dfrac{-5+\sqrt{29}}{2\sqrt2}+2\pi n\ ,\ \ n\in Z\\\\x=\dfrac{\pi}{4}\pm arccos\dfrac{-5+\sqrt{29}}{2\sqrt2}+2\pi n\ ,\ \ n\in Z\ \ -\ Otvet$

$2)\ \ sinx+cosx=1+sinx\cdot cosx$

Способ решения такой же.

Замена: $t=sinx+cosx\ ,\ \ 2sinx\cdot cosx=t^2-1\ \ ,\ \ sinx\cdot cosx=\dfrac{t^2-1}{2}\ .$

$t=1+\dfrac{t^2-1}{2}\ \ ,\ \ 2t=2+t^2-1\ \ ,\ \ t^2-2t+1=0\ ,\ \ (t-1)^2=0\ \to \ t=1\\\\sinx+cosx=1\ \ \to \ \ \ \sqrt2\cdot cos(x-\dfrac{\pi}{4})=1\ \ ,\ \ cos(x-\dfrac{\pi}{4})=\dfrac{1}{\sqrt2}\ ,\\\\\\x-\dfrac{\pi}{4}=\pm \dfrac{\pi}{4}+2\pi n \ \ ,\ \ \ x=\dfrac{\pi}{4}\pm \dfrac{\pi}{4}+2\pi n\ ,\ n\in Z\ \ -\ Otvet$

lizapogorelaia66: помоги с задачами по географии пожалуйста!! последние две , умоляю

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Русский язык, автор: asiat811281mailru

поставьте нв месте пропуска тире там,гдк это необходимо чистота...лучшая красота. несебр...этокаменный небольшой остров.ночь...темна и тиха. вьюга...началась быстро. село солотча...страна талантливых людей. дорога пустынна

2 года назад

Предмет: Русский язык, автор: желанная1

Запеши сочитание слоя.Подчеркнем за главную букву

2 года назад

Предмет: Русский язык, автор: maya42gsy

как пишется экскурсовод или экскурсовод или как

ДАЮ 30 баллов;!!!!!!! срочно!!!!!!!!!!!!! решать самим​

Ответы

ДАЮ 30 баллов;!!!!!!! срочно!!!!!!!!!!!!! решать самим