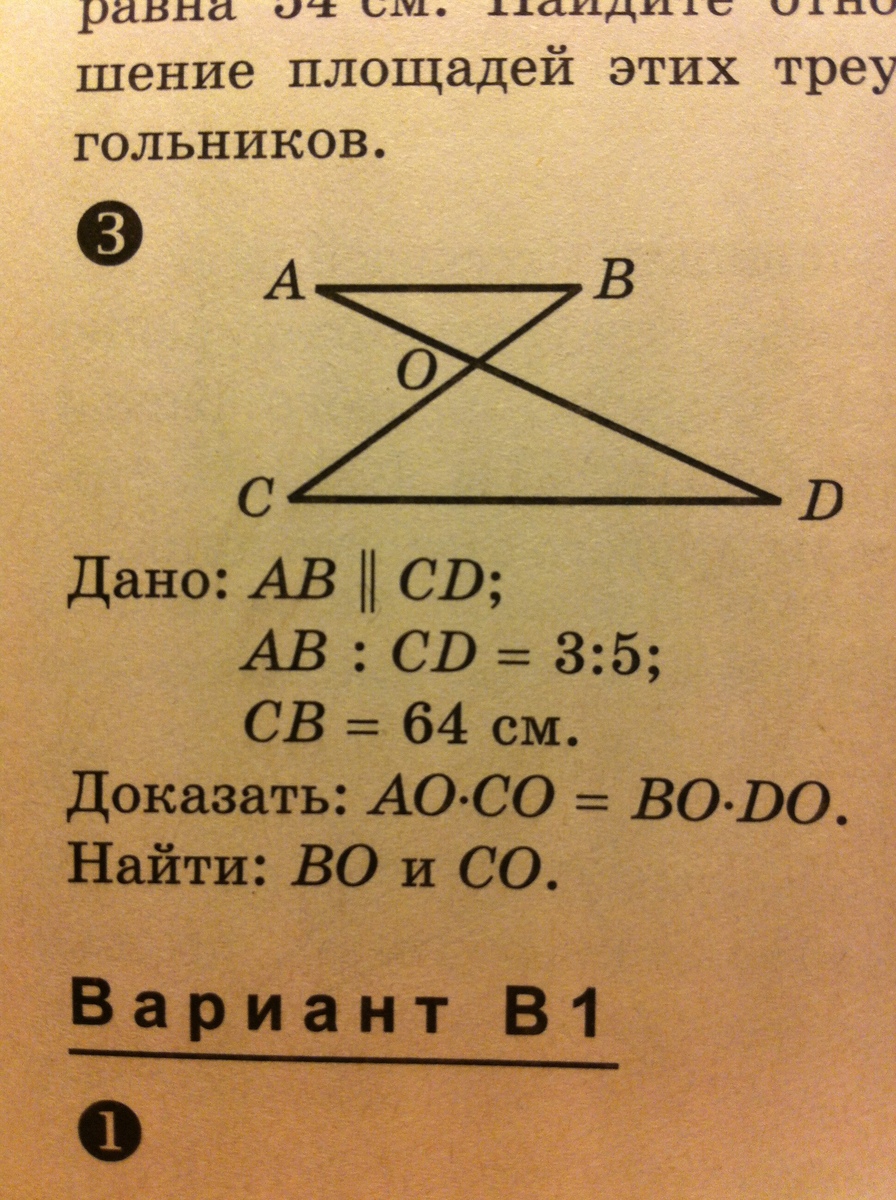
Дано:AB параллельно CD AB:CD=3:5 CB=64см Доказать:AO*CO=BO*DO Найти BO и CO.

∠ОАВ = ∠ODC как накрест лежащие при пересечении параллельных прямых АВ и CD секущей AD,
∠АОВ = ∠DOC как вертикальные, значит
ΔАОВ подобен ΔDOC по двум углам.

AO : DO = BO : CO ⇒
AO · CO = BO · DO - доказано.

Пусть ВО = х, тогда СО = 64 - х.
BO : CO = AB : CD
x : (64 - x) = 3 : 5
5x = 3(64 - x)
5x = 192 - 3x
8x = 192
x = 24
ВО = 24 см
СО = 64 - 24 = 40 см