В треугольнике ABC: A(5; 7), B(7; -4), C(15; 16). Отрезок АК делит площадь треугольника на две равные части. Найди координаты точки К. Ответ: К ​

Ответ:

К(11;6)

Объяснение:

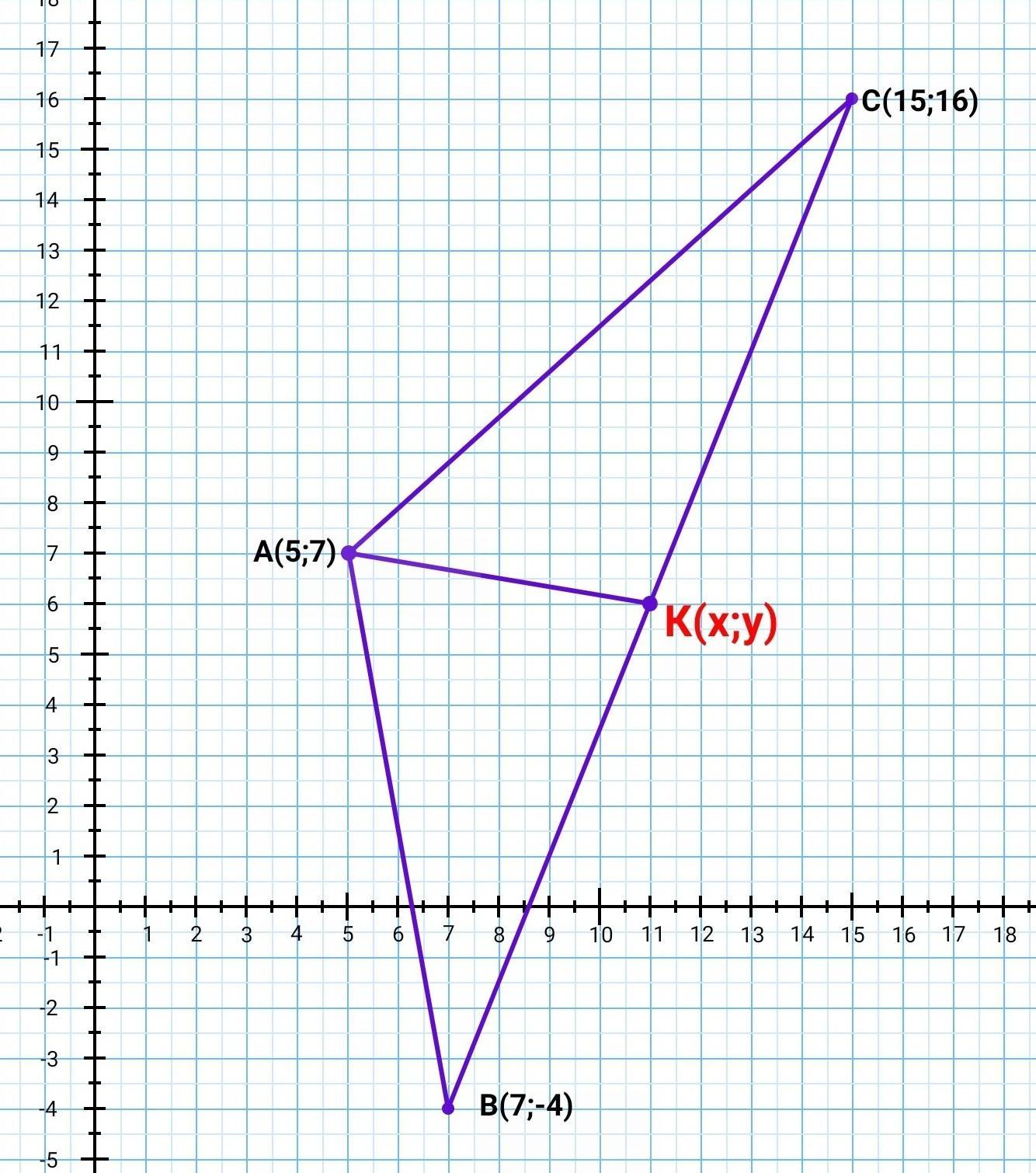
В △ABC: A(5; 7), B(7; -4), C(15; 16).

Отрезок АК делит площадь треугольника на две равные части.

Найти: координаты точки К.

Решение.

Известно, что медиана треугольника делит его на две равные части. Следовательно, АК - медиана.

Медиана - это отрезок соединяющий вершину треугольника с серединой противолежащей стороны.

Точка К(х;у) - середина ВС.

Найдём координаты середины отрезка ВС.

• Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.