Предмет: Геометрия,
автор: adriatutunnik
у трикутнику ABC відомо що c=90 AC=8см. BC=6см знайдіть sin кута A cos кута A tg кута B ctg кута B
Ответы
Автор ответа:
1
Ответ:
sin∠A = 0,6
cos∠A = 0,8
ctg∠B = 0,75
Объяснение:
По теореме Пифагора найдем гипотенузу:
AB = √(AC² + BC²)
AB = √(8² + 6²) = √(64 + 36) = √100 = 10 см
- Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе:
- Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе:
- Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:
- Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему:
Приложения:
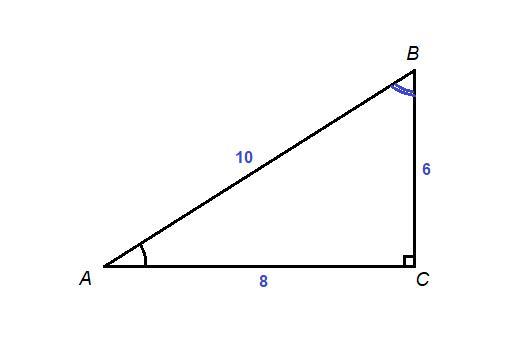
Интересные вопросы
Предмет: Другие предметы,
автор: ydhmjhy
Предмет: Русский язык,
автор: surovatkinam
Предмет: Русский язык,
автор: Lana1410
Предмет: Физика,
автор: nastya153592
Предмет: Математика,
автор: okarasev29