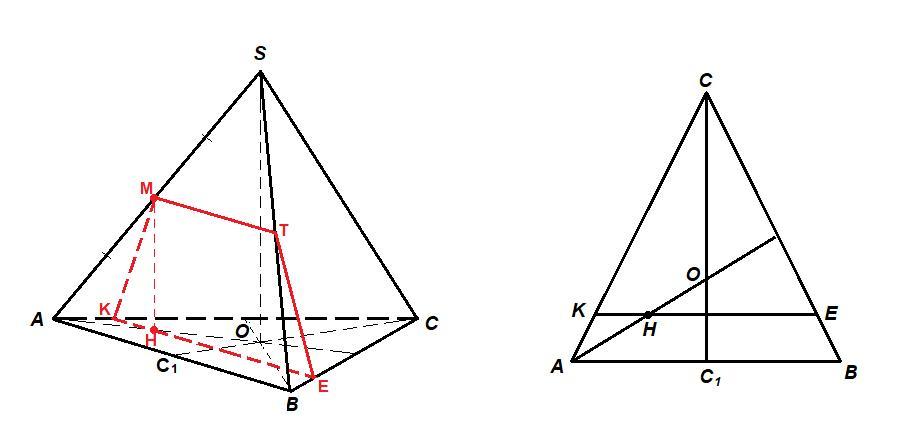
Задача 5. Постройте сечение правильной треугольной пирамиды SABC плоскостью, перпендикулярной высоте CC1 основания и проходящей через середину ребра AS

Ответ:

На рисунке.

Объяснение:

Треубется построить сечение правильной треугольной пирамиды.

Сечение должно проходить через точку М - середину ребра AS, перпендикулярно СС₁ - высоте основания.

SO - высота пирамиды.

Построение:

1. В плоскости ASO проведем МН ║ SO (Н ∈ АО).

2. СС₁ - высота основания, значит СС₁⊥АВ.

Проведем через точку Н прямую, параллельную АВ.  К - точка пересечения этой прямой с АС, Е - точка пересечения с ВС.

КЕ - отрезок сечения.

3. Соединим точки М и К. МК - отрезок сечения.

• Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

АВ║КЕ, значит прямая АВ параллельна секущей плоскости.

Через прямую АВ проходит плоскость (SAB), которая пересекает секущую плоскость, значит линия пересечения секущей плоскости и (SAB) параллельна прямой АВ.

Проведем МТ║АВ.

4. Соединим точки Т и Е. МТ и ТЕ - отрезки сечения.

КМТЕ - искомое сечение.

Действительно, сечение проходит через середину ребра AS. Докажем, что оно перпендикулярно прямой СС₁.

СС₁⊥АВ, КЕ║АВ, значит СС₁⊥КЕ.

МН║SO, SO⊥(ABC),  ⇒  MH⊥(ABC), а значит МН⊥СС₁, лежащей в (АВС).

Признак перпендикулярности прямой и плоскости:

• если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна плоскости.

СС₁⊥КЕ, МН⊥СС₁, значит СС₁⊥(МКЕ).