Предмет: Геометрия,
автор: deidispy
1) найти расстояние от точки К до прямой а (рис. 238)
2) укажите равные треугольники
Найти: угол BCD (рис. 239)
Приложения:
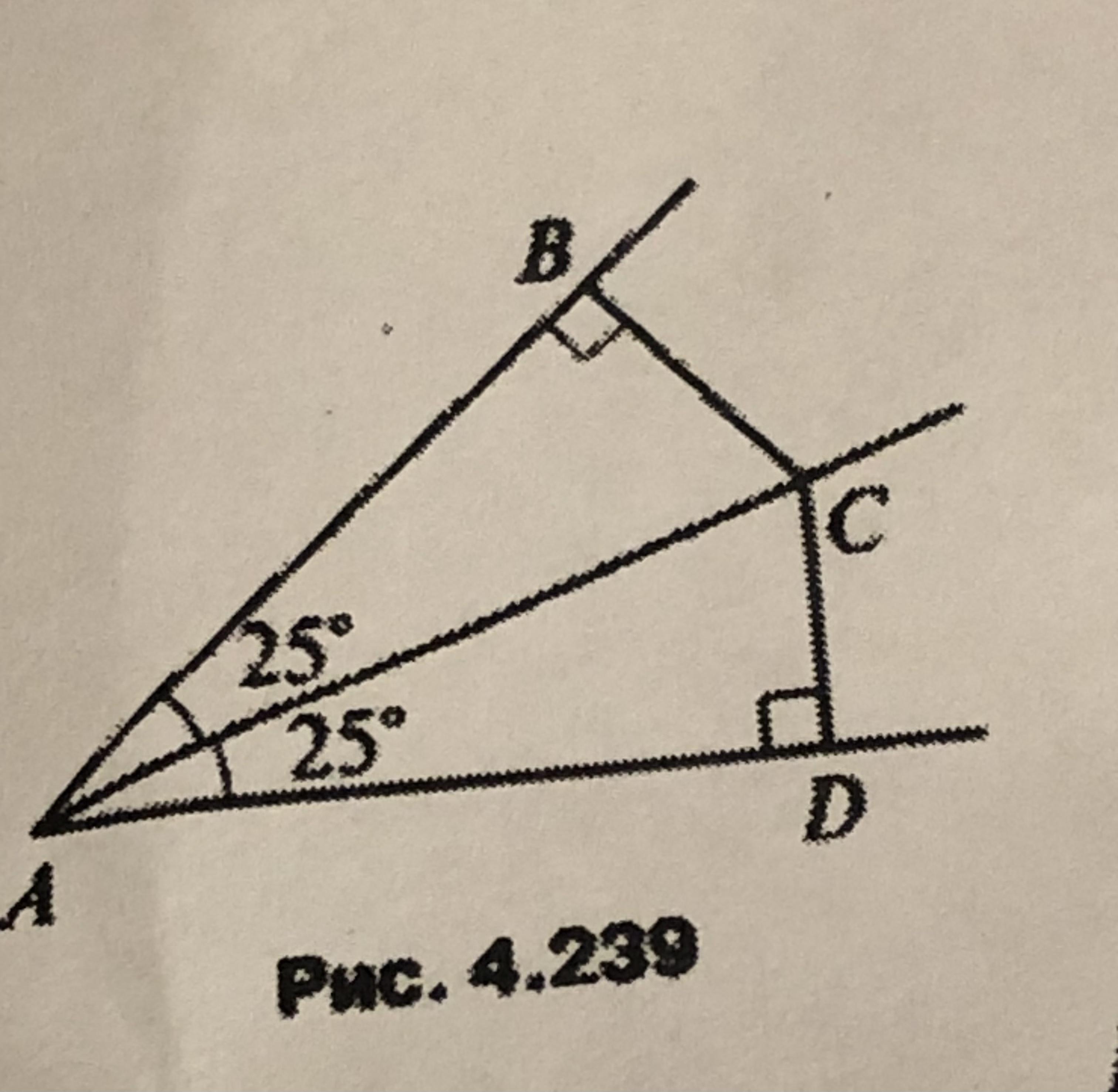
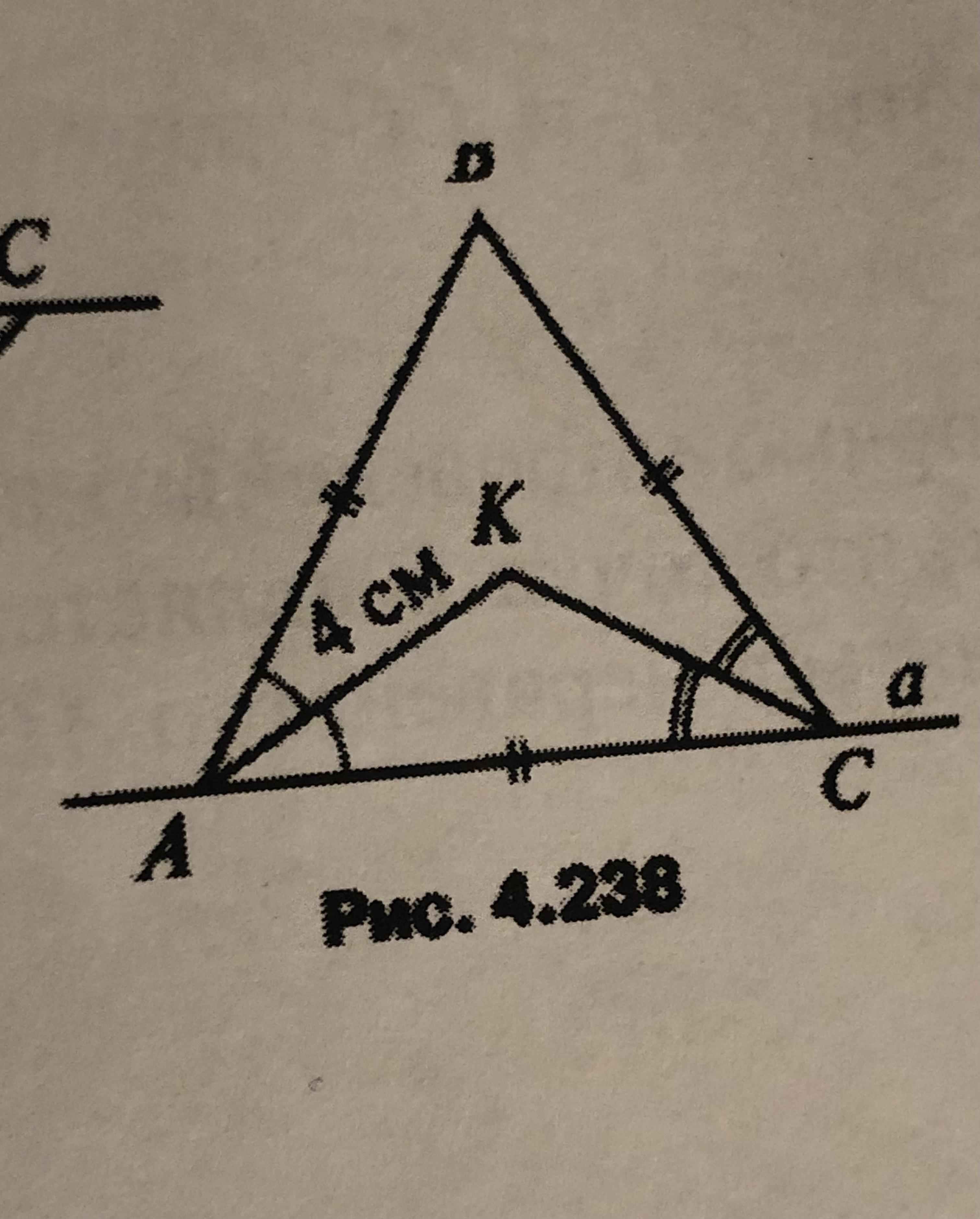
Ответы
Автор ответа:
2
Ответ:
1) 2 см. 2) ABC и ADC.
Объяснение:
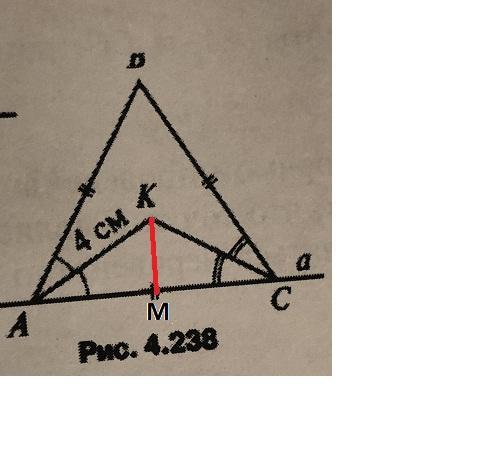
1) Смотрите рисунок, сделанный из Рис. 4.238.
Треугольник ABC - равносторонний, углы A = B = C = 60°.
Отрезки AK и CK - биссектрисы углов A и C.
Значит, углы KAC = KAB = KCB = KCA = 60°/2 = 30°
Треугольник AKC - равнобедренный с углами 30°, 30°, 120°.
Значит, высота этого треугольника, опущенная из точки K - она же биссектриса угла K и медиана отрезка AC.
Обозначим её KM. Тогда треугольник AKM - прямоугольный с углами 30°, 60°, 90° и гипотенузой AK = 4 см.
Катет KM против угла 30° равен половине гипотенузы:
KM = AK/2 = 4/2 = 2 см.
2) Рис. 4.239.
Равные треугольники - ABC и ADC.
По двум углам CAB = CAD = 25°; ABC = ADC = 90°
И общей стороне AC.
Приложения:
Интересные вопросы
Предмет: Технология,
автор: AnastasiaSims
Предмет: Русский язык,
автор: МиссКрис11
Предмет: Окружающий мир,
автор: милана460
Предмет: Английский язык,
автор: sergey77729
Предмет: Окружающий мир,
автор: yuliyashvecova