Помогите пожалуйста !!!!!!!!
Задание 1.
Окружность задана уравнением (x - 3)² + (y + 4)² = 25. Составьте уравнение окружности, которая симметрична заданной окружности относительно:
а) точки (−1; 3) (15 баллов);
б) оси абсцисс (15 баллов).

а) Из задания определяем радиус заданной окружности R = √25 = 5 и координаты центра – пусть это точка А(3; -4).

Находим точку B, симметричную точке A(3; -4) относительно точки C(-1; 3).

Пусть B(xB; yB) — точка, симметричная точке A относительно точки C.

Тогда x_C=(x_A+x_B)/2

 Отсюда x_B=2x_C-x_A=2*(-1)-3= -5.

Аналогично находим y_B=2y_C-y_A=2*3-(-4)= 10.

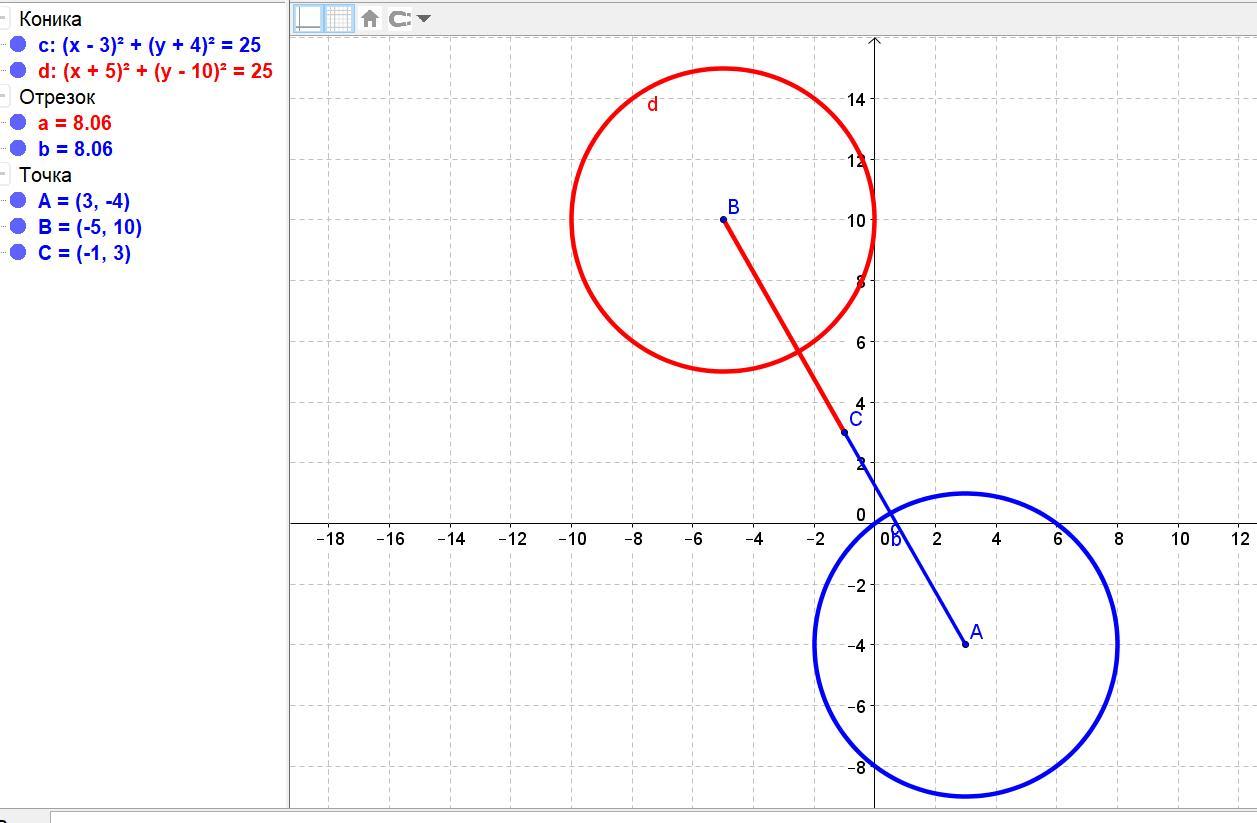
Ответ: окружность, которая симметрична заданной окружности относительно точки (-1; 3) имеет уравнение (x + 5)² + (y - 10)² = 25.

б) При симметрии относительно оси абсцисс абсцисса центра сохраняется, а знак ординаты меняется на противоположный.

 Ответ: (x - 3)² + (y - 4)² = 25.