Помогите пожалуйста!!!




Построй график функции и называет его свойства!

Ответ:

смогла решить только a, в b у меня странный график получается

Объяснение:

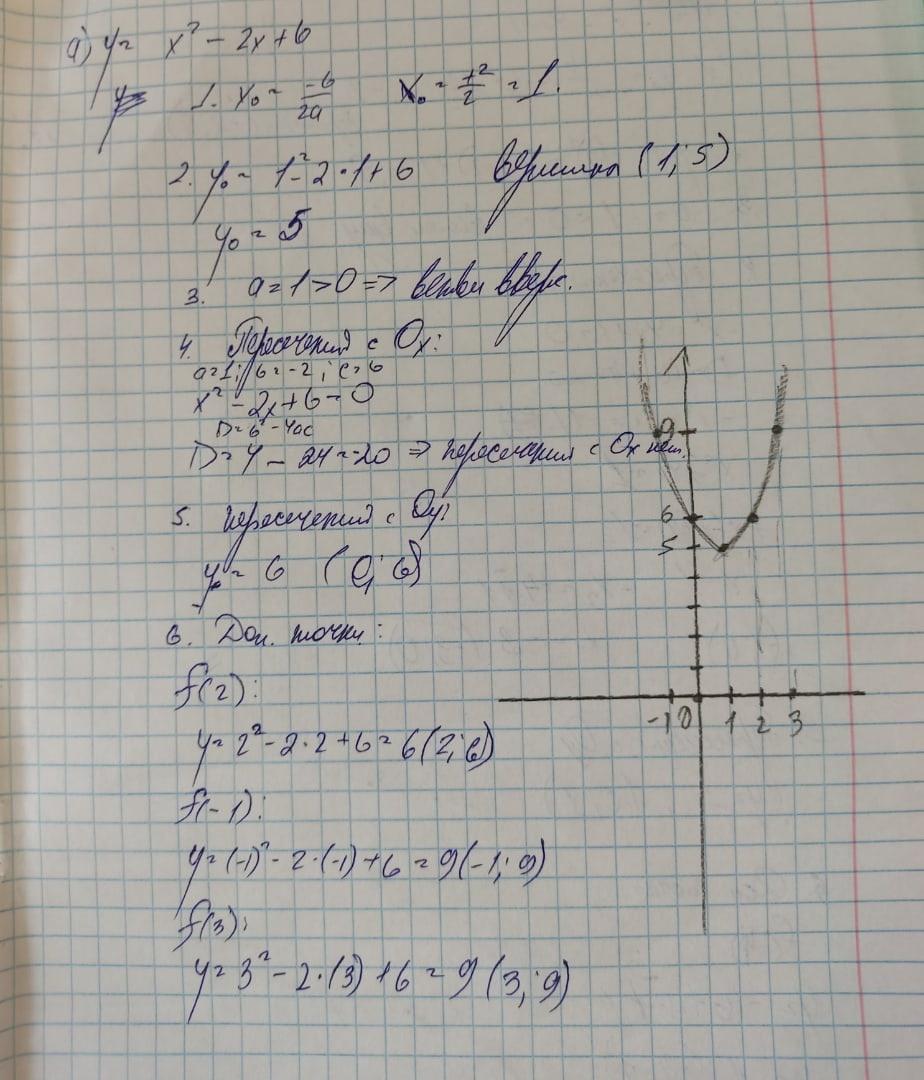
Ответ:

В решении.

Объяснение:

Построить график функции и указать её свойства:

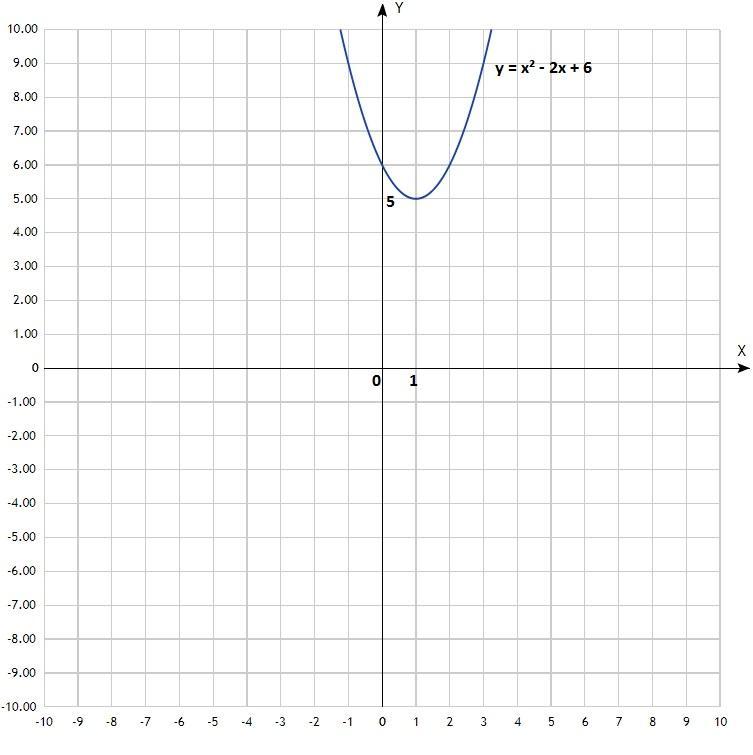
а) у = х² - 2х + 6;

Уравнение квадратичной функции, график - парабола, ветви направлены вверх.

Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

     Таблица:

х  -1     0     1     2     3

у   9    6     5     6     9

По вычисленным точкам построить параболу.

1) Найти область определения;

Область определения - это значения х, при которых функция существует, или это проекция графика функции на ось Ох.

Обозначается как D(f) или D(у).

Областью определения любой параболы является множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

D(у) = х∈R, или D(у) = х∈(-∞; +∞);

2) Найти множество значений функции;

Множество значений функции - это проекция графика на ось Оу.

Обозначается как Е(f) или Е(y).

Область значений параболы определяется координатами вершины, конкретно у₀, значение у вершины параболы.

Согласно графика, Е(y) = у∈[5; +∞);

3) Найти нули функции;

Нули функции - это значения х точек, в которых график пересекает ось Ох. При этом пересечении у всегда равен нулю.

Согласно графика, нулей данной функции не существует, так как парабола не пересекает ось Ох;

4) Найти промежутки знакопостоянства;

Согласно графика,

а) у > 0 (график выше оси Ох) на промежутках х∈(-∞; +∞);

б) у < 0 (график ниже оси Ох) не существует;

5) Найти промежутки возрастания функции;

Функция возрастает на промежутке х∈(1; +∞);

6) Найти промежутки убывания функции;

Функция убывает на промежутке х∈(-∞; 1).

7) у max. не существует;

   у min. = 5.

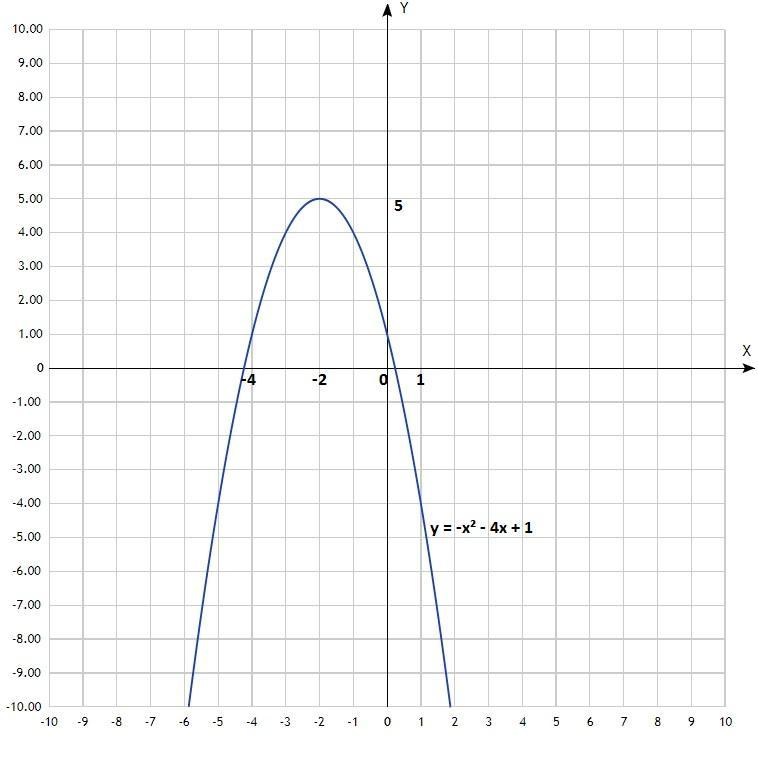
б) у = -х² - 4х + 1;

Уравнение квадратичной функции, график - парабола, ветви направлены вниз.

Придать значения х, подставить в уравнение, вычислить у, записать в таблицу.

     Таблица:

х  -5     -4     -3     -2     -1      0      1

у  -4       1      4      5      4      1      -4

По вычисленным точкам построить параболу.

1) Найти область определения;

Область определения - это значения х, при которых функция существует, или это проекция графика функции на ось Ох.

Обозначается как D(f) или D(у).

Областью определения любой параболы является множество всех действительных чисел, потому что она проецируется на любую точку оси Ох.

D(у) = х∈R, или D(у) = х∈(-∞; +∞);

2) Найти множество значений функции;

Множество значений функции - это проекция графика на ось Оу.

Обозначается как Е(f) или Е(y).

Область значений параболы определяется координатами вершины, конкретно у₀, значение у вершины параболы.

Согласно графика, Е(y) = у∈[5; -∞);

3) Найти нули функции;

Нули функции - это значения х точек, в которых график пересекает ось Ох. При этом пересечении у всегда равен нулю.

Приравнять к нулю и решить квадратное уравнение:

-х² - 4х + 1 = 0/-1

х² + 4х - 1 = 0

D=b²-4ac = 16 + 4 = 20        √D=√(4*5) = 2√5

х₁=(-b-√D)/2a

х₁=(-4-2√5)/2

х₁= -2 - √5 ≈ -4,2;                

х₂=(-b+√D)/2a

х₂=(-4+2√5)/2

х₂= -2 + √5 ≈ 0,2;

Согласно графика, нули данной функции: (-2-√5; -2+√5);

4) Найти промежутки знакопостоянства;

Согласно графика,

а) у>0 (график выше оси Ох) на промежутках х∈(-2-√5; -2+√5);

б) у<0 (график ниже оси Ох) на промежутках х∈(-∞; -2-√5)∪(-2+√5; +∞);

5) Найти промежутки возрастания функции;

Функция возрастает на промежутке х∈(-∞; -2);

6) Найти промежутки убывания функции;

Функция убывает на промежутке х∈(-2; +∞).

7) у max. = 5;

   у min. = не существует.