Предмет: Математика, автор: mus1ctv

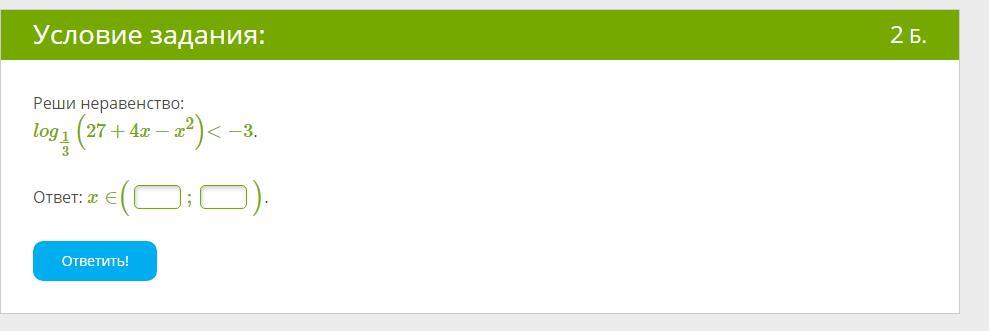
Решить неравенство с логарифмом.
Даю 20 баллов.

Приложения:

Ответы

Автор ответа: DrRichtofen

$log_{\frac{1}{3}}(27+4x-x^{2}) < -3$

$log_{\frac{1}{3}}(27+4x-x^{2}) < log_{\frac{1}{3}}27$

т.к 1/3>1, то

$\right. 27+4x-x^{2} > 27$

$4x-x^{2} > 0\\x(x-4) < 0\\$

Ответ: x∈(0;4)

mus1ctv: можете ещё решить?

mus1ctv: в скобке (8+5x-x2) остальное всё тоже самое

DrRichtofen: Ты можешь создать ещё раз вопрос? Я не могу здесь тебе полностью написать ответ

Автор ответа: Аноним

$\displaystyle log{_\frac{1}{3} } (27+4x-x^2) < -3, x \in (2-\sqrt{31},2+\sqrt{31})\\ \\27+4x-x^2 > (\frac{1}{3})^-^3\\ \\27+4x-x^2 > 3^3\\ 27+4x-x^2 > 27\\4x-x^2 > 0\\x(4-x) > 0\\\\\left \{ {{x > 0} \atop {4-x > 0}} \right. \rightarrow \left \{ {{x > 0} \atop {x < 4}} \right. \rightarrow x \in (0,4)\\\\\left \{ {{x < 0} \atop {4-x < 0}} \right. \rightarrow \left \{ {{x < 0} \atop {x > 4}} \right. \rightarrow \oslash\\\\ x \in (0,4)$