Предмет: Математика,
автор: None632
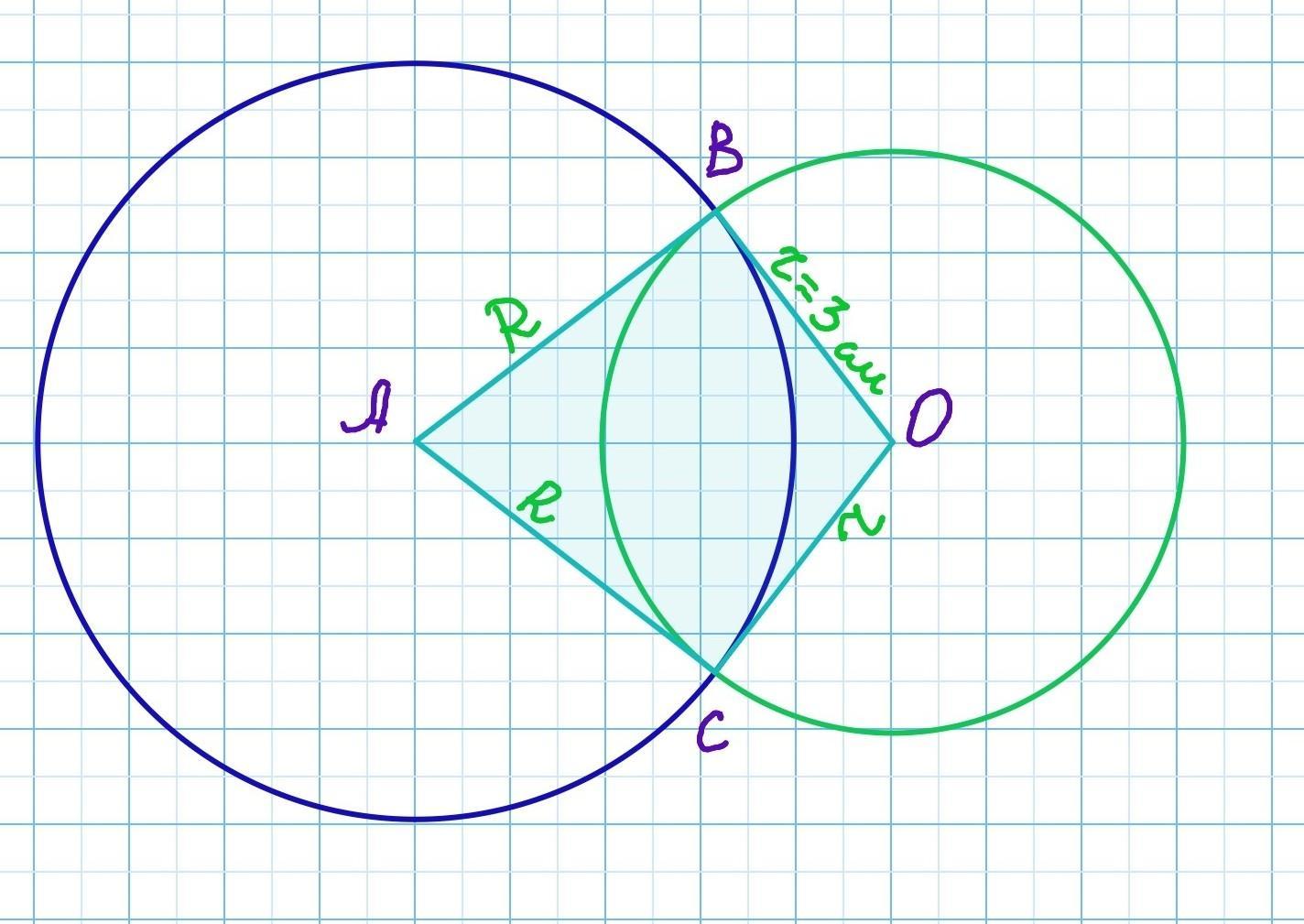
1273. На рисунке 8.12 изображены две пересекающиеся окружности с центрами в точках А и О. Диаметр окружности с центром в точке А равен 10 см, а радиус окружности с центром в точке О равен 3 см. Найдите периметр четырехугольника ABOC. Можете написать как это подробно решить
Приложения:

irewqw:
D=10
ооойййй
D= 10см R=3см P=(3×2)+(5×2)=16 см Ответ:P=16 см
Ответы
Автор ответа:
15
Ответ:
Периметр четырёхугольника АВОС равен 16 см.
Пошаговое объяснение:
Стороны ВО и СО четырехугольника АВОС являются радиусами окружности с центром в точке О. ВО=СО=r=3см
Стороны АВ и АС четырехугольника АВОС являются радиусами окружности с центром в точке А.
АВ=АС=R
Диаметр окружности с центром в точке А по условию задачи равен 10 см.
Так как радиус окружности равен половине диаметра, то радиус окружности с центром в точке А равен:
R=d/2=10/2=5см.
Периметр четырёхугольника равен сумме всех его сторон.
см
Приложения:
спс
Интересные вопросы
Предмет: Русский язык,
автор: нюша266
Предмет: Английский язык,
автор: Всезнайка8967
Предмет: Беларуская мова,
автор: тварь6
Предмет: Биология,
автор: Кетрин303
Предмет: Биология,
автор: kristinakarpaeva74