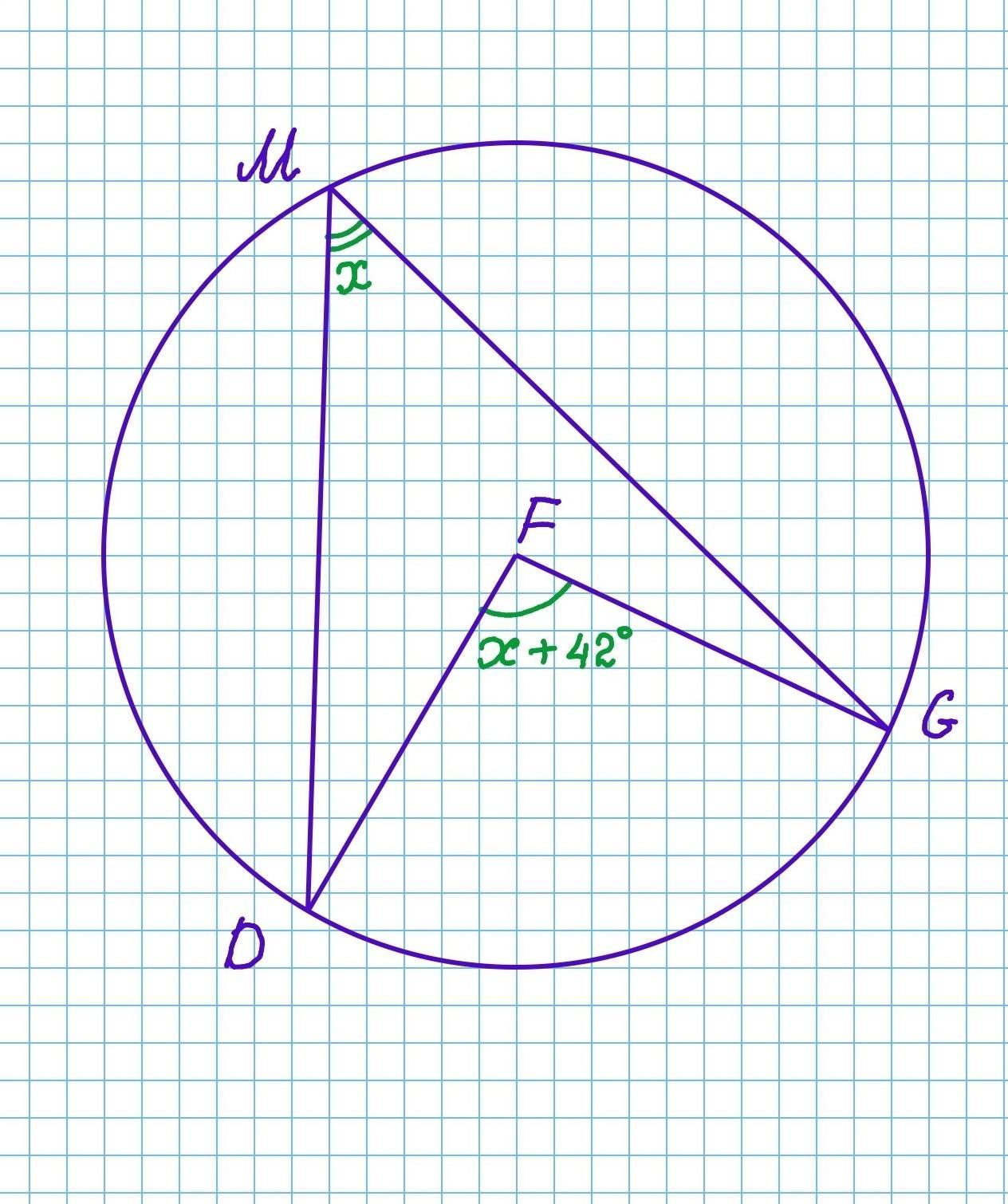
Определи, какими могут быть градусные меры центрального угла 

D

F

G

DFG и вписанного угла, опирающегося на дугу 

D

G

DG, если известно, что 

∠

D

F

G

∠DFG на 

42

°

42° больше вписанного угла.

Определи, какими могут быть градусные меры центрального угла ∠DFG и вписанного угла, опирающегося на дугу DG, если известно, что ∠DFG на 42° больше вписанного угла.

Ответ:

Градусная мера центрального угла равна 84°,

Градусная мера центрального угла равна 84°, градусная мера вписанного угла равна 42°.

Объяснение:

• Центральный угол - это угол, вершина которого является центром окружности, а стороны - это радиусы, пересекающие окружность в двух разных точках.
• Вписанный угол - это угол, вершина которого лежит на окружности, а стороны пересекают окружность.
• Вписанный угол равен половине центрального угла, опирающегося на ту же дугу.

Решение

∠DFG - центральный угол, опирающийся на дугу DG.

∠DMG - вписанный угол, опирающийся на дугу DG.

Пусть вписанный угол DMG равен х°, тогда центральный угол DFG равен (х+42)°.

Так как центральный угол в два раза больше вписанного, составляем уравнение:

∠DFG=2•∠DMG

x+42=2•x

x=42°

∠DMG=42°, ∠DFG=42+42=84°.