Предмет: Геометрия, автор: abbat2001

Решите пожалуйста С РИСУНКОМ

Дан прямоугольный треугольник, разность гипотенузы и меньшего катета составляет 15 см. Один из углов равен 60°. Найти гипотенузу и меньший катет

Ответы

Автор ответа: lilyatomach

1

Ответ:

Меньший катет равен 15 см, а гипотенуза равна 30 см.

Объяснение:

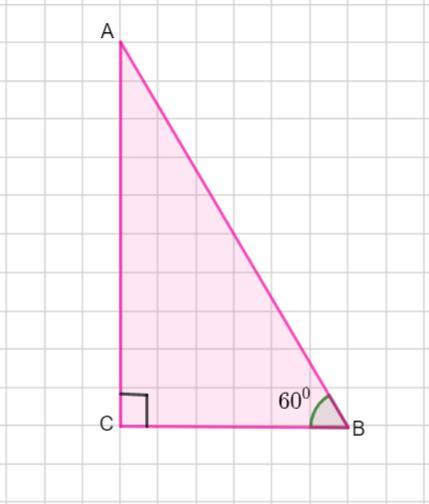
Рассмотрим Δ АВС - прямоугольный. ∠С =90°.

АВ - гипотенуза.

∠В =60°

Сумма острых углов прямоугольного треугольника равна 90°. Тогда

∠А =90 °- 60° = 30°.

Тогда катет ВС - наименьший, так как лежит напротив наименьшего угла.

По условию разность между гипотенузой и наименьшим катетом равна 15 см, то есть АВ -ВС =15 см.

По свойству катета, лежащего напротив угла в 30 °

$BC = \dfrac{1}{2} AB$

Пусть ВС = х см. Тогда АВ =2х см. Так как АВ -ВС =15 см, то составляем уравнение:

$2x-x=15;\\x=15$

Значит, катет ВС = 15 см, а гипотенуза

$AB =2\cdot 15 =30$ см.

#SPJ1

Приложения:

Предыдущий вопрос

Следующий вопрос

Интересные вопросы

Предмет: Другие предметы, автор: Makovka93

СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА!!!
Нотариус N-ского нотариального округа Елена Петровна Фролова неоднократно подвергалась проверкам нотариальной палаты N- области и Главного управления Минюста России по N- области, в ходе которых отмечались недостатки в ее профессиональной деятельности. При проведении последней проверки в апреле 2010 г. в ее работе был выявлен ряд нарушений. С 09 по 31 января 2014 года нотариус Е.П.Фролова работала без реестра регистрации нотариальных действий, поскольку только 01 февраля 2014 года она получила его в нотариальной палате. Совершенные ранее нотариальные действия были занесены ею в данный реестр позднее, причем с нарушениями. На день проверки в реестре отсутствовали подписи и адреса некоторых клиентов, не были вписаны отдельные нотариальные действия, которые совершались нотариусом. И не были указаны реквизиты документов, которые копировались. Данные нарушения Е.п.Фролова объяснила тем, что в начале 2014 г.она не могла получить реестр регистрации нотариальных действий, так как исполнительный директор нотариальной палаты N-области находился на больничном. Также нотариус Е.П.Фролова не вводила в единую информационную систему нотариата в информационной структуре Российской Федерации (далее – еНОТ) завещания, отмененные доверенности и не вела учет бланков единого образца строгой отчетности для выполнения нотариальных действий в электронном виде. 15 декабря 2013 года в нотариальной палате N-области прошло совещание по вопросу внедрения системы еНОТ, на котором присутствовали все нотариусы, в том числе и Е.П.Фролова, а также программист, рассказавший о данной программе. На совещании было доведено до сведения нотариусов, что система осваивается просто, и каждого нотариуса научат пользоваться ею. Но, по словам Е.П.Фроловой, она не смогла освоить еНОТ, поскольку плохо владеет компьютером. В марте 2014 года Е.П.Фролова перестала нотариально удостоверять сделки по отчуждению недвижимости, предлагая клиентам услуги по составлению договоров купли-продажи недвижимости, которые сама и оформляла. За данный вид услуг ею взималась плата, которая не отражалась в реестре регистрации нотариальных действий. Содержание информационного стенда в нотариальной конторе не отвечало требованиям к организации нотариального облуживания, утвержденным правлением Федеральной нотариальной палаты России (протокол от 13-14 ноября 2003 года № 09/03). Он не содержал перечня документов, необходимых для оформления прав на наследство, размеры тарифов и льготы за совершение нотариальных действий, адреса других нотариальных контор, нотариальной палаты N- области. Е.П.Фролова вела прием граждан четыре дня в неделю. В пятницу, по ее словам, оказывались услуги клиентам вне помещения нотариальной конторы. При этом в документах, подтверждающих совершение нотариальных действий, не указаны адреса выездов на дом. На заседании нотариальной палаты N-области Е.П.Фролова в основном согласилась с замечаниями, указанными в акте проверки. Обещала исправить имеющиеся в работе недостатки. Выявленные нарушения она считает несущественными, поскольку никто из граждан с жалобами на ее деятельность не обращался. Она убеждена, что проверка должна носить рекомендательный характер со стороны руководства палаты. Вместе с тем нотариальная палата обратилась в N-ский районный суд с иском о лишении права нотариальной деятельности занимающегося частной практикой нотариуса Е.П.Фролову.

Задания

Оцените ситуацию с точки зрения действующего законодательства и норм этики, принятых в нотариальном сообществе.
Какие нормы законодательства и профессиональной этики нотариуса были нарушены?
Каковы меры реагирования профессионального сообщества нотариусов на нарушения законодательства и норм профессиональной этики со стороны его членов? Каковы последствия нарушения норм действующего законодательства и профессиональных этических норм в данной ситуации.?

2 года назад

Предмет: Другие предметы, автор: kjgh

1) Кравотечения это
а)истечение крови из кровеносных сосудов при нарушении целостности их стенок;
b) Потеря организмом какого либо количество крови;
в)выход крови наружу из поврежденных органов

2 года назад

Предмет: Русский язык, автор: настя15251

найди здесь ошипку
1. 2. 3. 4. 5 6. 7 8 9 10

2 года назад

Предмет: Математика, автор: Sevdasuleymanova313

(X-3)•(2x-8)=0как найти

8 лет назад

Предмет: Математика, автор: nur531

Здравствуете помогите пожалуйста (3дм3см3мм+5см8мм)•5???

8 лет назад