СРОЧНО!!!
решите пожалуйста!!!
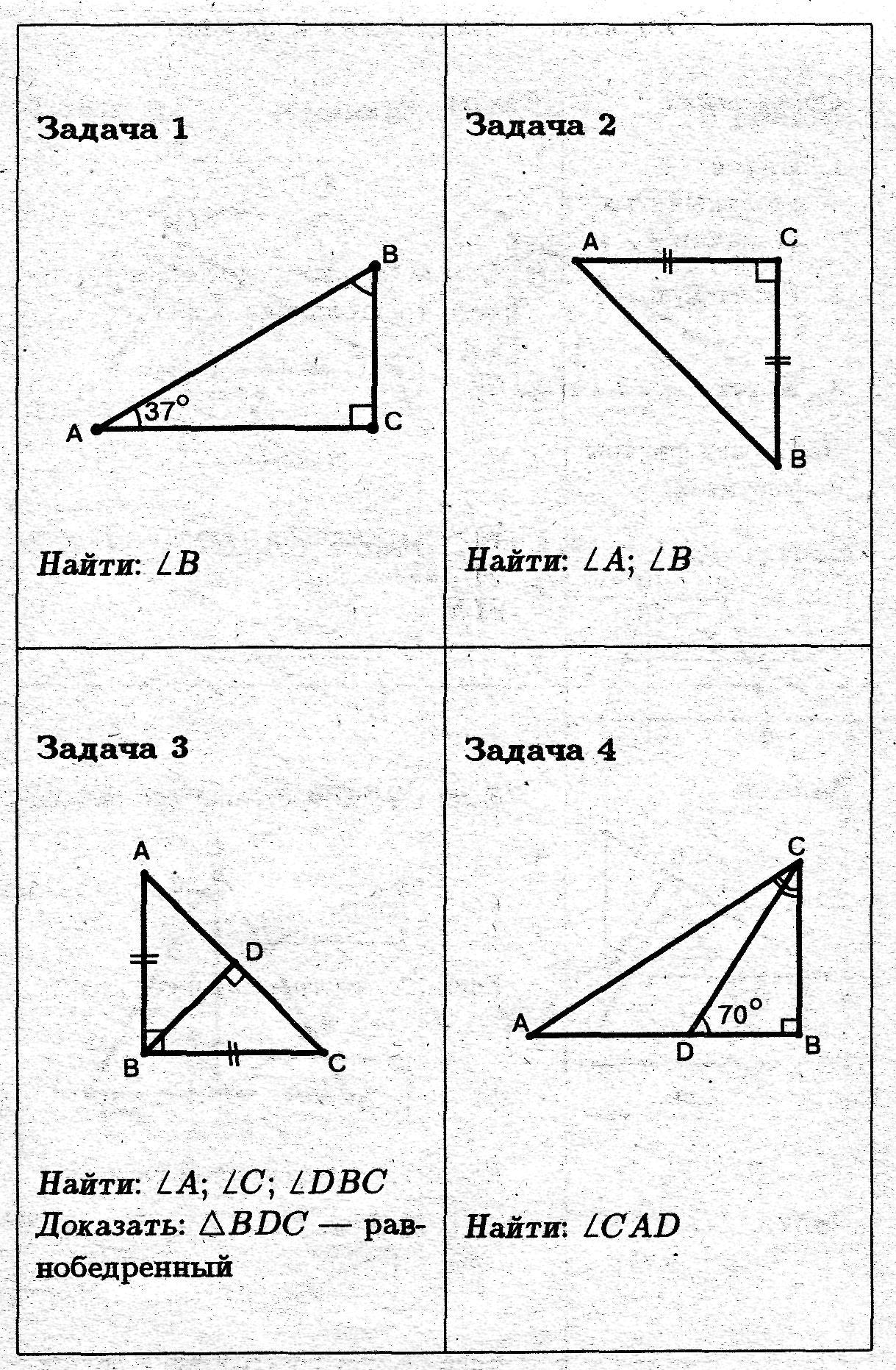
Ответы
Ответ:
1) ∠В =53°; 2) ∠А =45°, ∠В =45 °; 3) ∠А=45°, ∠С =45°, ∠DВС =45°;
4) ∠CАD=50°.
Объяснение:
1) На первом рисунке задан Δ АВС - прямоугольный.
∠С=90°, ∠А =37°. Надо найти ∠ В.
Так как сумма острых углов прямоугольного треугольника равна 90°, то
∠В =90°-37°=53°
2) На втором рисунке задан Δ АВС - прямоугольный,
так как ∠С =90°. Если АС =ВС , то треугольник равнобедренный.
В равнобедренном треугольнике углы при основаниии равны и их сумма в этой задаче равна 90°.
Тогда ∠А=∠В =90°: 2 =45 °.
3) На третьем рисунке дан Δ АВС - прямоугольный, ∠В =90° и равнобедренный, так как АВ =ВС по рисунку.
Если треугольник равнобедренный, то углы при основании равны. И их сумма равна 90°. Тогда ∠А =∠С =90°: 2 =45°
В этом треугольнике проведена высота BD . Значит, ∠BDС =90°, если ∠С =90° и ΔBDС - прямоугольный. Сумма острых углов равна 90°. Тогда если ∠С =45°, то ∠DВС =90°-45°=45°.
4) На рисунке 4 задан Δ АВС - прямоугольный. В нем проведена биссектриса CD, так как ∠ACD =∠BCD .
Рассмотрим ΔCВD - прямоугольный. Сумма острых углов равна 90° в прямоугольном треугольнике. Тогда если ∠CDВ =70°, то
∠BCD=90 °-70°=20°.
∠ACD =∠BCD =20°
∠CDВ -внешний угол Δ АCDВ . Внешний угол треугольника равен сумме двух внутренних не смежных с ним.
∠CАD=70° -20°=50°
#SPJ1