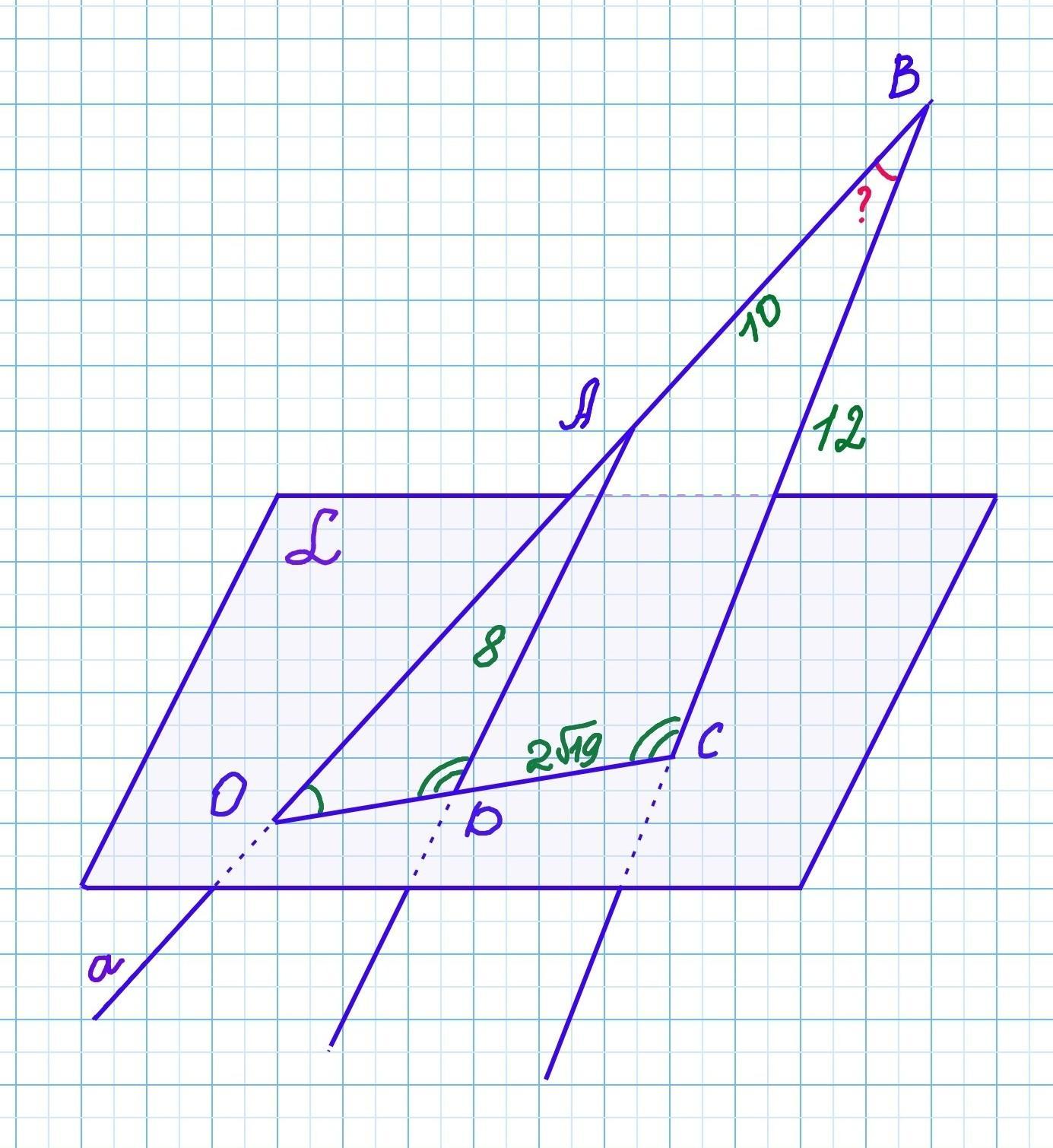
Прямая a пересекает плоскость альфа (a) в точке O. Из точек A и B, лежащих на прямой a по одну сторону от точки O, проведены параллельные прямые, пересекающие плоскость альфа (a) в точках D и C соответсвенно. Найдите косинус угла между прямыми AB и BC, если AD=8, BC=12, AB=10, DC=2корень из 19

Ответ:

Косинус угла между прямыми АВ и ВС:

Пошаговое объяснение:

Прямая a пересекает плоскость в точке O. Из точек A и B, лежащих на прямой a по одну сторону от точки O, проведены параллельные прямые , пересекающие плоскость в точках D и C соответсвенно (AD II BC).  AD=8, BC=12, AB=10, DC=2√19.

Найдём косинус угла между прямыми AB и BC.

РЕШЕНИЕ

1) Треугольник OBC подобен треугольнику OAD (по двум углам).

У них: ∠О - общий, ∠ODA = ∠OCD - как соответственные углы при параллельных прямых AD и BC и секущей OC.

Из подобия треугольников следует пропорциональность соответственных сторон:

OB = OA+ AB = OA + 10

OC = OD + DC = OD + 2√19

Тогда:

OA = 20 ед, следовательно OB = 20+10 = 30 ед

OD = 4√19 ед, следовательно OC = 4√19+2√19=6√19 ед

2) Выразим косинус ∠В из теоремы косинусов:

Подставим найденные значения и найдём косинус угла между прямыми AB и BC:

#SPJ1