Предмет: Алгебра,
автор: kaseta345
Знайти проміжки зростання і спадання та екстремуми функції f(x) = x^2+ 2,5/x+2
Приложения:
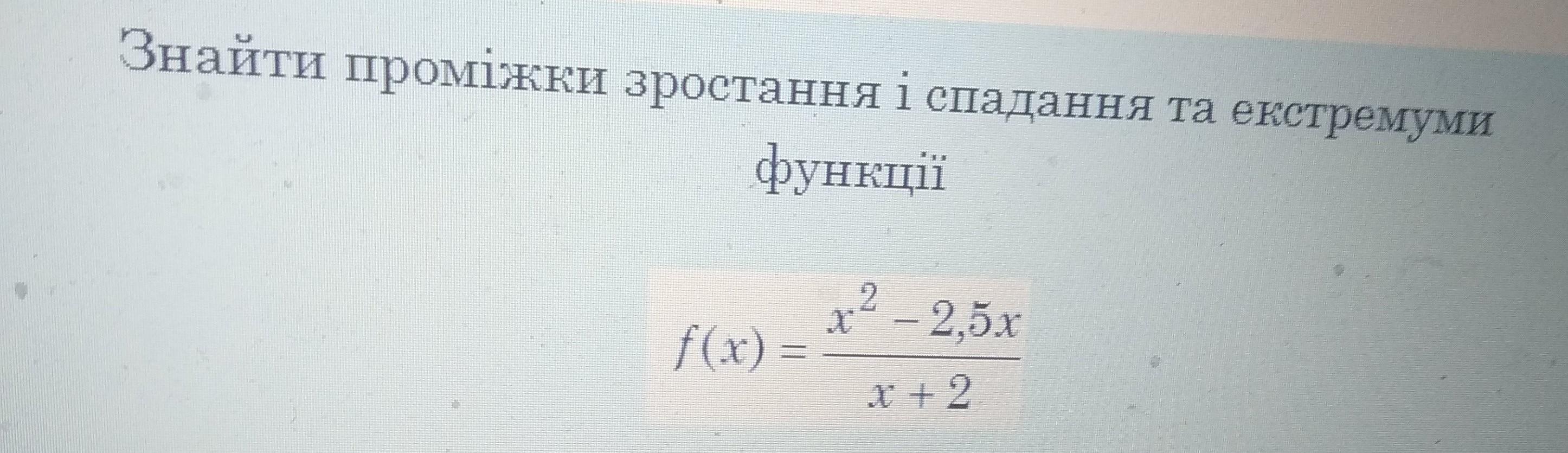
Ответы
Автор ответа:
3
найдем производную функции f(x)=(x²-2.5x)/(x+2).
(xⁿ)'=n*xⁿ⁻¹
(u*v)'=u'v+uv'
f'(x)=((2х-2.5)(х+2)-1*(х²-2.5х))/(х+2)²
(2х²+4х-2.5х-5-х²+2.5х)/(х+2)²
(х²+4х-5)/(х+2)²=0
найдем критические точки.
x+2≠0
х≠-2
х²+4х-5=0, по теореме, обратной теореме Виета х=1;х=-5;
_______-5___-2__1_______
+ - - +
функция убывает при х∈[-5; -2) и при х∈(-2;5];
точка максимума х=-5
максимум f(-5)=(25+12.5)/(-5+2)=-12.5
точка минимума х=1
f(1)=(1-2.5)/(1+2)=-1.5/3=-0.5
kaseta345:
Объясните, пожалуйста,в точке x=-2 функция разве недифференцируемая?
конечно. нет. она же там не определена.
Спасибо за помощь,я уже понял
пожалуйста
Интересные вопросы
Предмет: Английский язык,
автор: айша60
Предмет: Русский язык,
автор: rramanovskaya
Предмет: Русский язык,
автор: volodiako4ev
Предмет: Химия,
автор: SaveMe18
Предмет: Алгебра,
автор: bandera34