Предмет: Геометрия,
автор: inka382
Помогите пожалуйста!!!
Определи, или треугольник является прямоугольным, если даны его стороны длиной!
Приложения:
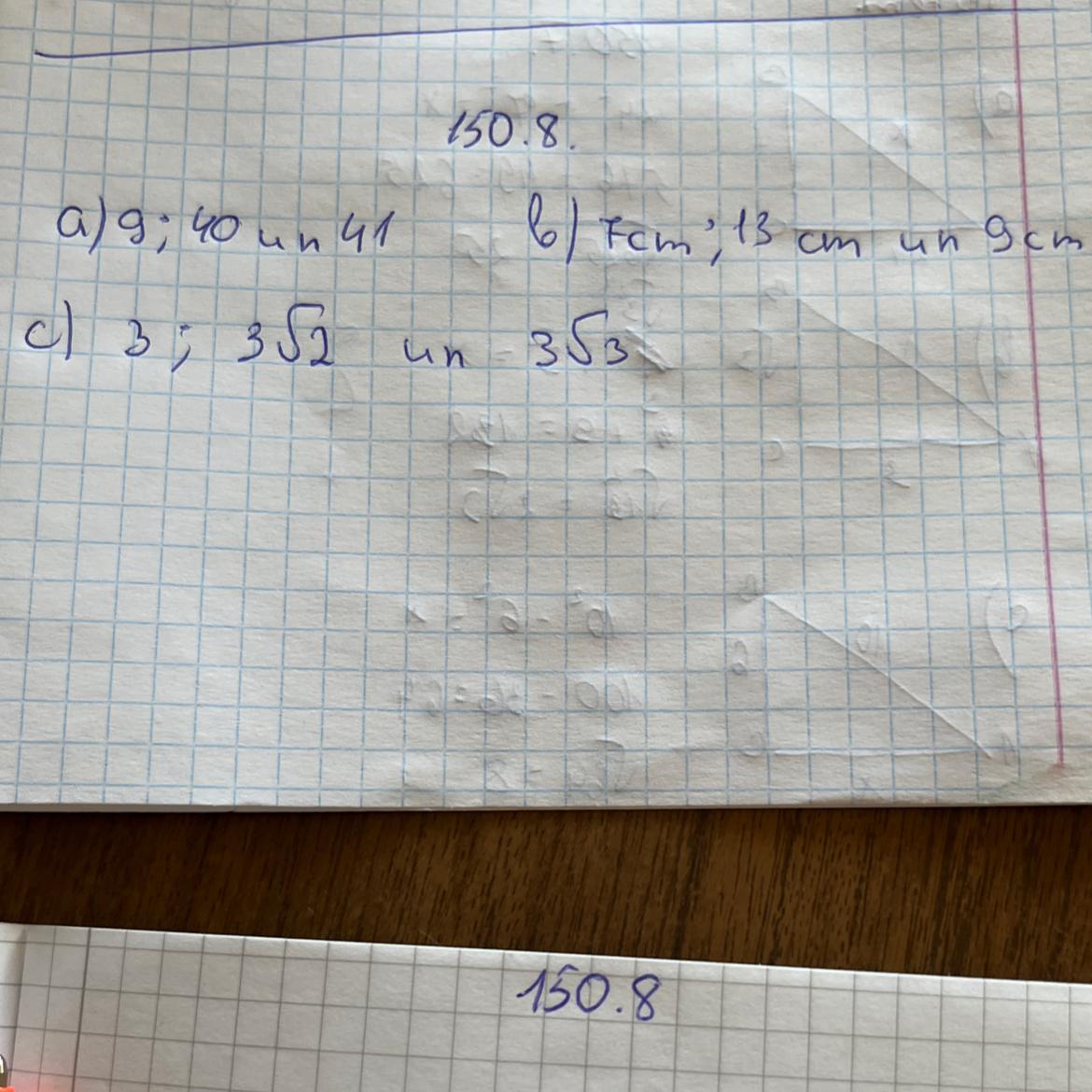
zmeura1204:
1) √(9²+40²)=41 да.
2) √(7²+9²)=√130; √130≠13 нет.
3) √(3²+(3√2)²)=√(9+18)=√27=3√3; да.
Спасибо
Ответы
Автор ответа:
0
Ответ:
a)=
+
⇒да
b)+
⇒нет
с)(3√3)²=(3√2)²+3²⇒да
Автор ответа:
1
Ответ:
а) прямоугольный треугольник;
b) не прямоугольный треугольник;
с) прямоугольный треугольник.
Объяснение:
Если треугольник прямоугольный, то должна выполняться теорема Пифагора:
a² + b² = c²
Где a и b - катеты, а с - гипотенуза.
Гипотенуза - это самая длинная сторона в треугольнике.
Проверим, выполняется ли равенство, подставив стороны в формулу теоремы Пифагора.
а) 9² + 40² = 41²
1681 = 1681
Значит этот треугольник прямоугольный.
b) 7² + 9² = 13²
130 ≠ 169
Таким образом, это не прямоугольный треугольник.
с) 3² + =
27 = 27
Значит этот треугольник прямоугольный.
Интересные вопросы
Предмет: Русский язык,
автор: Kotuk228myr
Предмет: Русский язык,
автор: Зайка20061
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: numa5
Предмет: Английский язык,
автор: Аноним