Предмет: Алгебра, автор: ughmejii

найдите частное решение дифференциального уравнения первого порядка
y'=xe^-y, y(1)=0
очень срочно нужно, пожалуйста.​

Приложения:

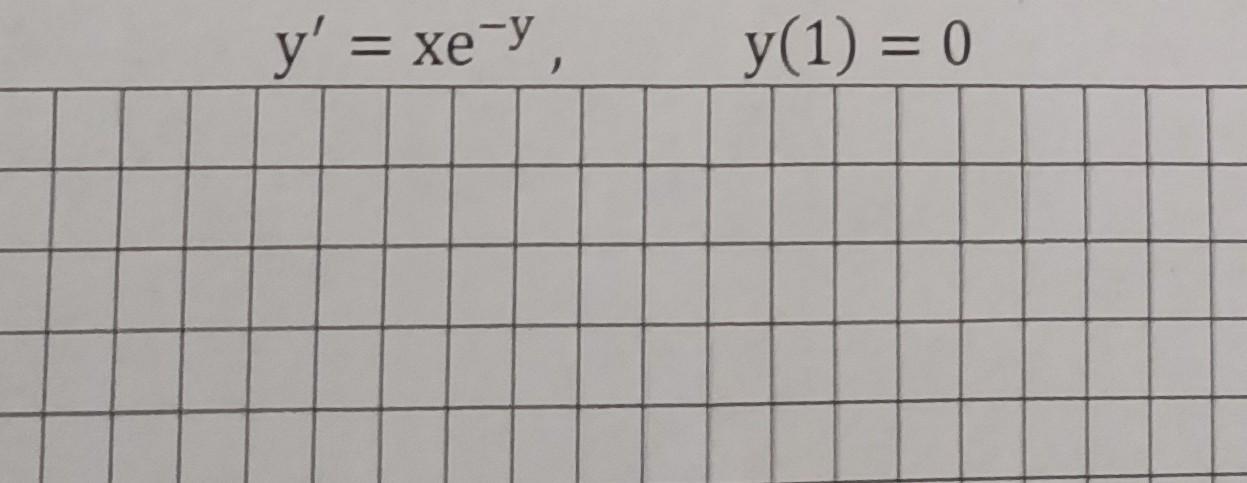
Ответы

Автор ответа: NNNLLL54
1

Ответ:

y'=xe^{-y}\ \ ,\ \ \ y(1)=0

Это дифф. ур-е с разделяющимися переменными, так как оно имеет

вид   y'=f_1(x)\cdot f_2(y)  .

\displaystyle y'=\frac{dy}{dx}\ \ ,\ \ \frac{dy}{dx}=x\cdot e^{-y}\ \ ,\ \ \ \frac{dy}{e^{-y}}=x\, dx\ \ ,\\\\\\\int \frac{dy}{e^{-y}}=\int x\, dx\ \ \ \ ,\ \ \ \ \int e^{y}\, dy=\int x\, dx\ \ ,\ \ \ e^{y}=\frac{x^2}{2}+C\ \ ,

\underline{y=ln\Big(\dfrac{x^2}{2}+C\Big)\ }   общее решение д.у.

Подставим начальные условия, найдём частное решение .

y(1)=0:\ e^0=\dfrac{1^2}{2}+C\ \ \ \Rightarrow \ \ \ 1=\dfrac{1}{2}+C\ \ \ ,\ \ \ C=\dfrac{1}{2}

y=ln\Big(\dfrac{x^2}{2}+\dfrac{1}{2}\Big)\ \ \Rightarrow \ \ \ \boxed{y=ln\dfrac{x^2+1}{2}}    частное решение д.у.

Предыдущий вопрос
Следующий вопрос
Интересные вопросы
Предмет: Русский язык, автор: кристина1577
помогите пожалуйста написать сочинение по картине ю.ракша проводы ополчения))
2 года назад
Предмет: Другие предметы, автор: Аноним
Географические координаты:
Горы Килиманджаро
Г.Бразилиа
Срочноо!!!
2 года назад
Предмет: Русский язык, автор: BAUROROZBAEV
орфоэпия это что такое!!!!!!!;:%;*№:%( ?_(+_++_*?Г?:%У
2 года назад
Предмет: Математика, автор: Аноним
помогите 100 балов даю
8 лет назад
Предмет: Химия, автор: zafarhk484
Вычислите процентное содержание металлов в следующем минерале Ca и Ti в перовските CaTiO(3)
8 лет назад