Предмет: Геометрия,
автор: Аноним
Срочно, пожалуйста!
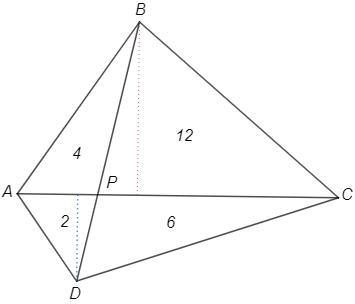
Диагонали четырехугольника ABCD пересекаются в точке P. Найти площадь треугольника АDP, если S ∆ABP = 4 см², S ∆BCP = 12 см², S ∆CDP = 6 см².
Ответы
Автор ответа:
1
Площади треугольников с равными высотами относятся как основания.
S(ABP)/S(BCP) =AP/PC =4/12 =1/3
S(ADP)/S(DCP) =AP/PC => S(ADP)/6 =1/3 => S(ADP)=2 (см^2)
Приложения:
Интересные вопросы
Предмет: Русский язык,
автор: maksimowdmitri
Предмет: Русский язык,
автор: анна1767
Предмет: Другие предметы,
автор: gwer123
Предмет: Математика,
автор: alieva2112
Предмет: Русский язык,
автор: ksusagajnullina86