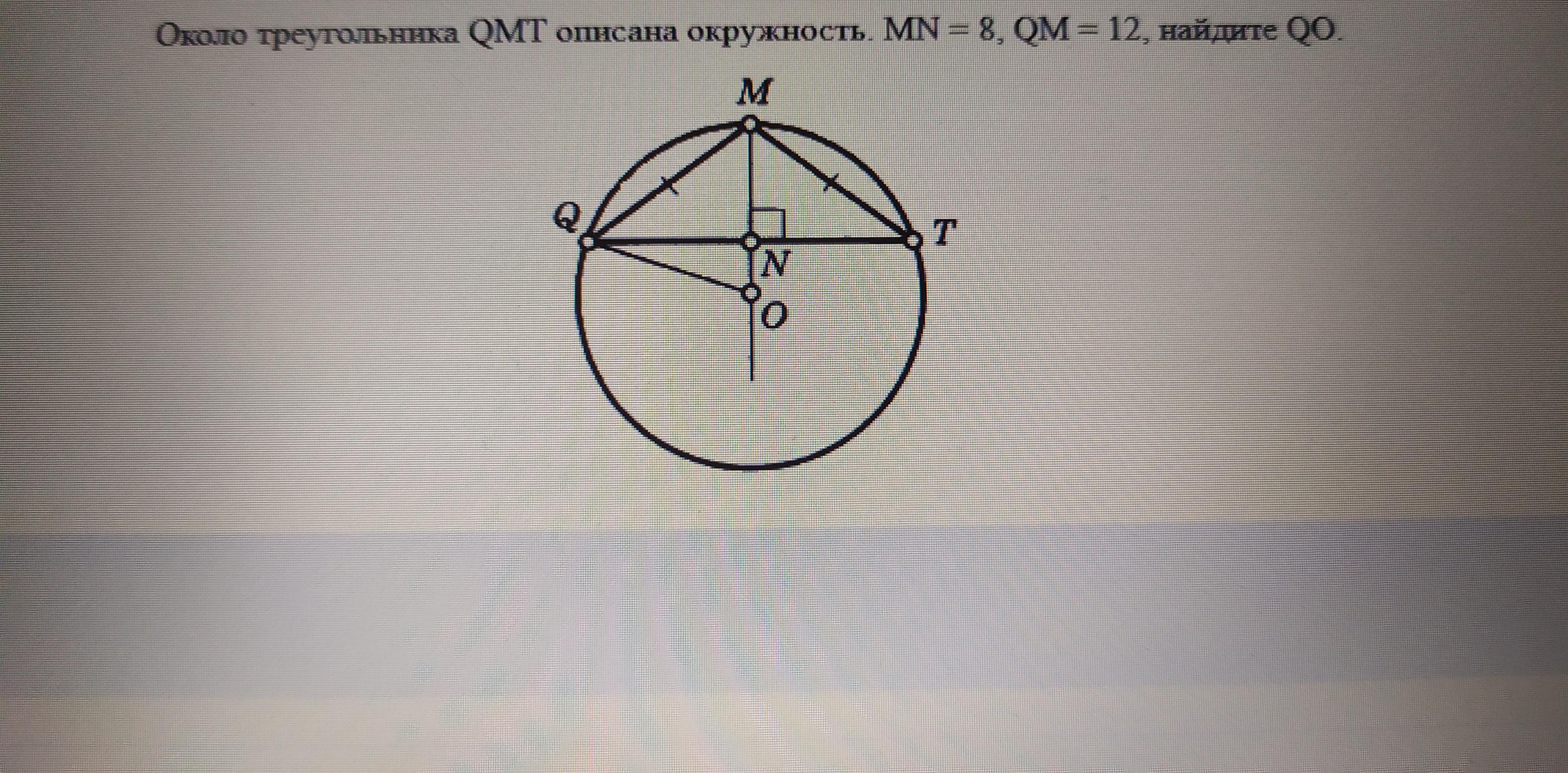
Около треугольника QMT описана окружность. MN = 8, QM = 12, найдите QO.

Ответ:

Длинна отрезка QO ( радиус описанной окружности) равна

9 единиц

Примечание:

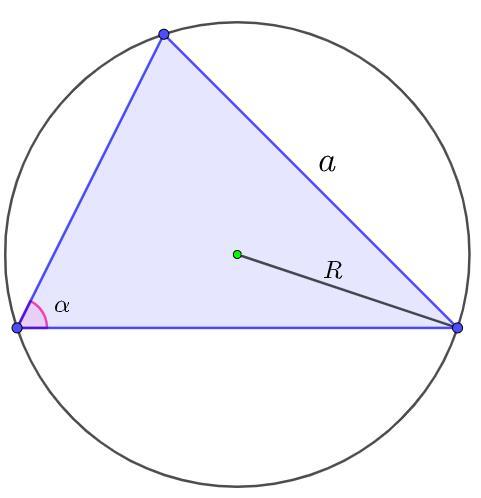
Следствие из теоремы синусов:

• R = a / (2 sin α)

Где:

• a - сторона треугольника
• R - радиус описанной окружности
• α - угол лежащий против стороны а

(смотрите приложение)

Объяснение:

Дано: QM = MT = 12, MN = 8, MN - высота, O - центр описанной окружности, QO - радиус описанной окружности

Найти: QO - ?

Решение:

Рассмотрим прямоугольный (по условию MN - высота)

треугольник ΔQMN.

По определению синуса в прямоугольном треугольнике:

• sin ∠MQT = MN / QM = 8 / 12 = (2/3)

По следствию из теоремы синусов для треугольника ΔQMT:

QO = MT / (2 sin ∠MQT) = 12 / (2 * (2/3) ) = 3 * 3 = 9 единиц

#SPJ1