Предмет: Математика, автор: normalded

Помогите пж!!! Вычислить площадь фигуры, ограниченной линиями

Приложения:

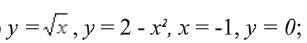
Ответы

Автор ответа: natalyabryukhova

Ответ:

Площадь фигуры, ограниченной линиями

y = √x, y=2 - x², x = -1, y = 0, равна $\displaystyle 2\frac{2}{3}$ ед.²

Пошаговое объяснение:

Вычислить площадь фигуры, ограниченной линиями:

y = √x, y=2 - x², x = -1, y = 0.

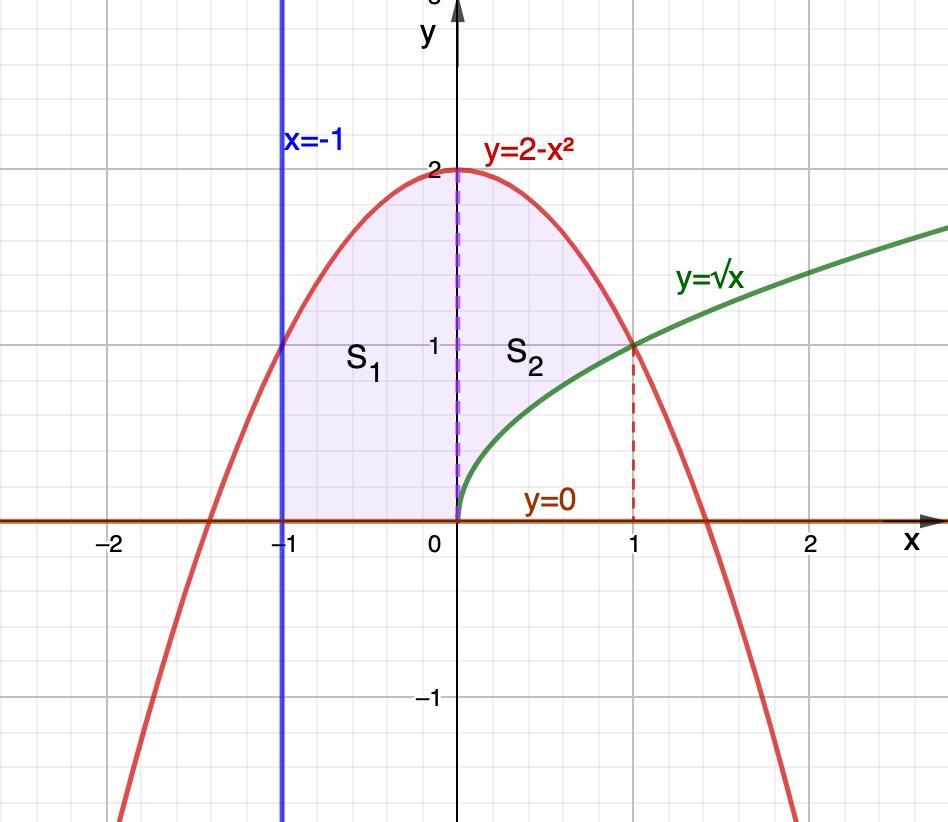
Построим графики и определимся с фигурой, площадь которой надо вычислить.

1. у = √х

- графиком является ветвь параболы, расположенная в первой четверти.

2. у = 2 - х²

- квадратичная функция, график - парабола с вершиной (0; 2), ветви вниз.

3. х = -1

- прямая, параллельная оси ординат.

4. у = 0

- это ось 0х.

Найдем абсциссу пересечения графиков y = √x и y=2 - x².

√x =2 - x²

√х + х² = 2

Очевидно, что здесь единственный корень

х = 1.

Выделим фигуру, ограниченную этими линиями.

Заметим, что искомую площадь можно найти как сумму двух площадей S₁ и S₂.

S = S₁ + S₂.

Площадь криволинейной трапеции равна:

$\boxed {S=\int\limits^b_a {(f_2(x)-f_1(x))} \, dx }$

Найдем площадь:

$\displaystyle S = \int\limits^0_{-1} {(2-x^2-0)} \, dx +\int\limits^1_0 {(2-x^2-\sqrt{x} )} \, dx =\\\\=\left(2x-\frac{x^3}{3}\right)\bigg|^0_{-1} +\left(2x-\frac{x^3}{3}-\frac{2x^{\frac{3}{2} }}{3} \right)\bigg|^1_{0} =\\\\=\left(0-\left(-2+\frac{1}{3}\right)\right)+\left(2-\frac{1}{3}-\frac{2}{3}-0\right)=\\ \\ =1\frac{2}{3}+1=2\frac{2}{3}$